CF1270I Xor on Figures

给定一个整数 $k$，以及一个 $2^k \times 2^k$ 的网格，每个格子中写有一个数，格子 $(i, j)$ 初始包含数字 $a_{ij}$。该网格被视为一个环面，即 $(i, 2^k)$ 右侧的格子是 $(i, 1)$，$(2^k, i)$ 下方的格子是 $(1, i)$。同时给定一个由 $t$ 个格子组成的“图形” $F$，其中 $t$ 是奇数。$F$ 不要求连通。 你可以进行如下操作：将 $F$ 平移到网格上的某个位置（只允许平移，不允许旋转和翻转），然后选择任意一个非负整数 $x$。之后，对于 $F$ 覆盖到的每个格子 $(i, j)$，将 $a_{ij}$ 替换为 $a_{ij} \oplus x$，其中 $\oplus$ 表示[按位异或运算](https://en.wikipedia.org/wiki/Bitwise_operation#XOR)。 更正式地，设 $F$ 由格子 $(x_1, y_1), (x_2, y_2), \dots, (x_t, y_t)$ 构成。你可以进行如下操作：选择任意 $x, y$ 满足 $1 \le x, y \le 2^k$，任意非负整数 $x$，对于每个 $i$ 从 $1$ 到 $t$，将 $(((x + x_i - 1)\bmod 2^k) + 1, ((y + y_i - 1)\bmod 2^k) + 1)$ 位置的数替换为 $a_{((x + x_i - 1)\bmod 2^k) + 1, ((y + y_i - 1)\bmod 2^k) + 1} \oplus x$。 你的目标是使所有格子中的数都变为 $0$。你能否做到？如果可以，求出最少需要多少次操作。

第一行包含一个整数 $k$（$1 \le k \le 9$）。 接下来的 $2^k$ 行，每行包含 $2^k$ 个整数 $a_{i1}, a_{i2}, \dots, a_{i2^k}$（$0 \le a_{ij} < 2^{60}$），表示网格第 $i$ 行的初始值。 接下来一行包含一个整数 $t$（$1 \le t \le \min(99, 4^k)$，$t$ 为奇数），表示图形的格子数。 接下来的 $t$ 行，每行包含两个整数 $x_i$ 和 $y_i$（$1 \le x_i, y_i \le 2^k$），表示图形中第 $i$ 个格子的位置。 保证所有格子互不相同，但不保证图形连通。

如果无法通过这些操作使所有格子的数都变为 $0$，输出 $-1$。 否则，输出一个整数，表示最少需要多少次操作。可以证明，如果可以使所有格子变为 $0$，则所需操作次数不会超过 $10^{18}$。

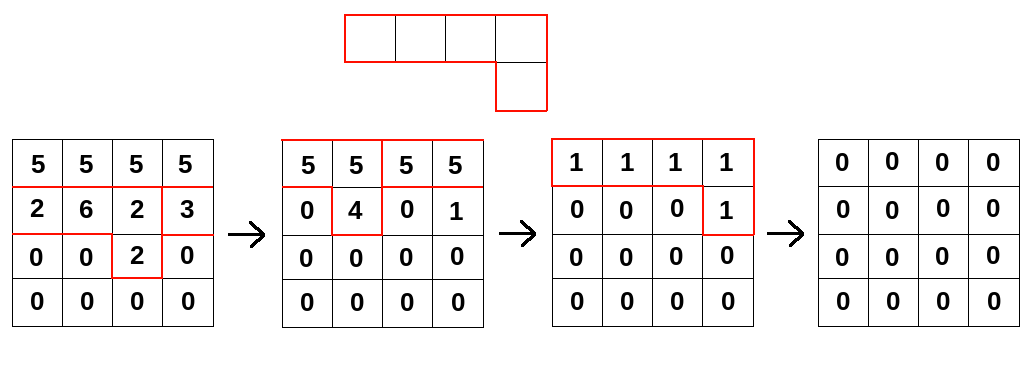
下图展示了样例中的图形和操作：  由 ChatGPT 4.1 翻译