CF1278D Segment Tree
题目描述
如题目名称所示,你需要处理一些关于线段和树的问题。
回忆一下,树是一个连通的无向图,且任意两点之间恰好有一条简单路径。
给定 $n$ 个线段 $[l_1, r_1], [l_2, r_2], \dots, [l_n, r_n]$,其中对于每个 $i$,都有 $l_i < r_i$。保证所有线段的端点都是整数,且所有端点互不相同——不存在两条线段起点相同、终点相同,或一条线段的起点等于另一条线段的终点的情况。
现在用这些线段生成一个有 $n$ 个顶点的图。若且仅若线段 $[l_v, r_v]$ 和 $[l_u, r_u]$ 相交,且没有一条线段完全包含在另一条线段内部,则在顶点 $v$ 和 $u$ 之间连一条边。
例如,$([1, 3], [2, 4])$ 和 $([5, 10], [3, 7])$ 这两对线段会连边,但 $([1, 2], [3, 4])$ 和 $([5, 7], [3, 10])$ 这两对线段不会连边。
请判断最终得到的图是否为一棵树。
输入格式
第一行包含一个整数 $n$($1 \le n \le 5 \times 10^5$),表示线段的数量。
接下来的 $n$ 行中,第 $i$ 行包含两个整数 $l_i$ 和 $r_i$($1 \le l_i < r_i \le 2n$),表示第 $i$ 条线段。
保证所有线段的端点两两不同。
输出格式
如果最终得到的图是一棵树,输出 "YES";否则输出 "NO"。
说明/提示
第一个样例对应的图如下:
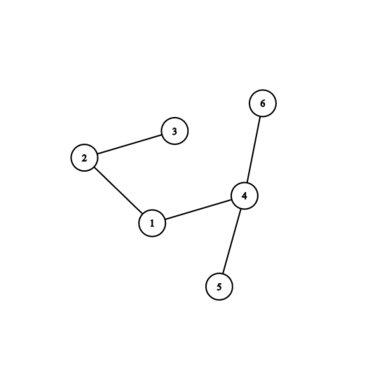
第二个样例对应的图如下:
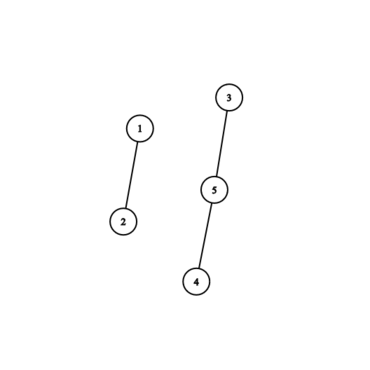
第三个样例对应的图如下:
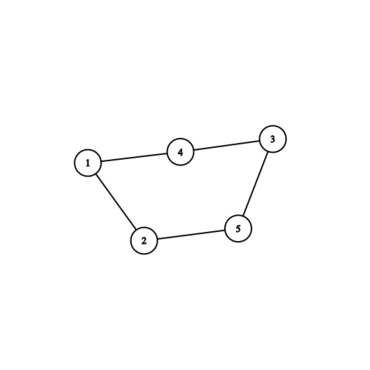
由 ChatGPT 4.1 翻译