CF1280E Kirchhoff's Current Loss

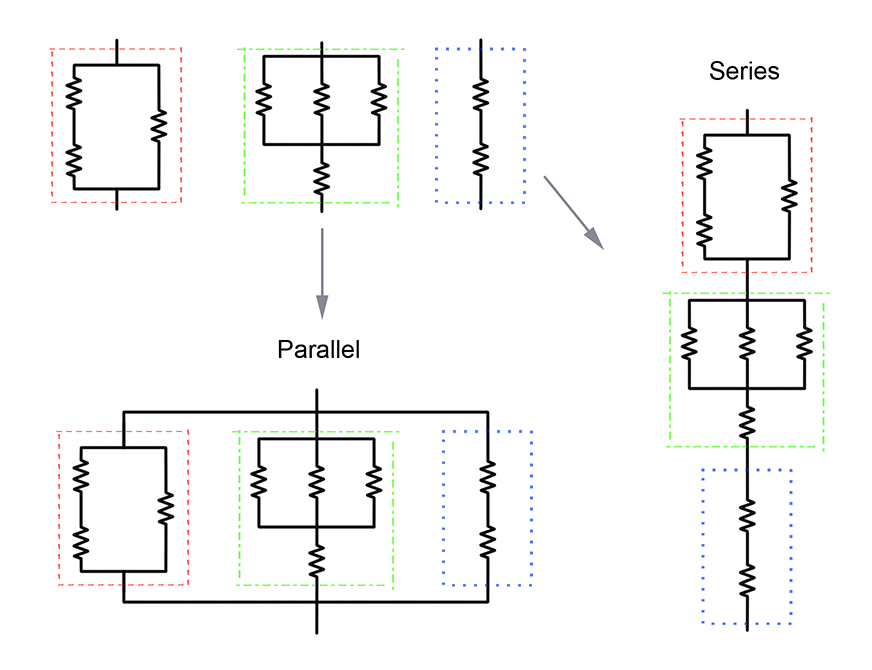
你的朋友 Kirchhoff 对当前的电子设计现状感到震惊。 “天哪！这个领域到底怎么了？这些电路太低效了！还有很大的提升空间。电气工程师们的课程一定讲得很糟糕。简直令人作呕。”他说。 他的负能量源源不断，但即使抱怨了这么多次，他还是没有“跃迁”去直接改变什么。 “这些电路的总电阻太大了。为什么要这样设计？这只会造成大量电阻器的浪费！他们整个领域如果能最大化设计的潜力，就能节省很多钱。为什么他们就不能尝试一些替代方案呢？” 他对电气工程系的抱怨频率让你心力交瘁，于是你决定亲自出马帮助他们。你打算编写一个程序，在保持电路布局和等效电阻不变的前提下，优化电路。 一个电路有两个端点，并与一个常数 $R$ 相关，称为其等效电阻。 我们考虑的电路由若干个单独的电阻器通过串联或并联组合而成，形成更复杂的电路。下图展示了电路串联和并联的组合方式。  根据你的朋友 Kirchhoff 的说法，通过如下方式可以很容易地计算组合电路的等效电阻： - 当将 $k$ 个等效电阻分别为 $R_1, R_2, \ldots, R_k$ 的电路串联时，组合后的等效电阻 $R$ 为它们的和： $$ R = R_1 + R_2 + \ldots + R_k. $$ - 当将 $k$ 个等效电阻分别为 $R_1, R_2, \ldots, R_k$ 的电路并联时，组合后的等效电阻 $R$ 满足： $$ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \ldots + \frac{1}{R_k}, $$ （假设所有 $R_i > 0$）；如果至少有一个 $R_i = 0$，则整个电路的等效电阻为 $R = 0$。 电路将用字符串表示。单个电阻器用星号“*”表示。对于更复杂的电路，假设 $s_1, s_2, \ldots, s_k$ 表示 $k \ge 2$ 个电路，则： - “( $s_1$ S $s_2$ S $\ldots$ S $s_k$ )” 表示它们的串联电路； - “( $s_1$ P $s_2$ P $\ldots$ P $s_k$ )” 表示它们的并联电路。 例如，“(* P (* S *) P *)” 表示如下电路： 给定一个电路，你的任务是为每个单独的电阻器分配电阻值，使其满足以下要求： - 每个电阻器的电阻值为非负整数； - 整个电路的等效电阻为 $r$； - 所有电阻器电阻值之和最小。 如果有 $n$ 个电阻器，你需要输出 $r_1, r_2, \ldots, r_n$（$0 \le r_i$，且 $r_i$ 为整数），其中 $r_i$ 是输入中第 $i$ 个出现的电阻器（从左到右）分配的电阻值。如果无法完成任务，也要说明。 如果可以完成，则保证最小电阻和不超过 $10^{18}$。

输入的第一行包含一个整数 $t$（$1 \le t \le 32000$），表示测试用例的数量。接下来的每一行描述一个测试用例。 每个测试用例包含一行，包含一个整数 $r$（$1 \le r \le 10^6$），后跟一个表示电路的字符串。保证字符串合法且符合上述描述。单独电阻器（符号“*”）的数量不少于 $1$ 且不超过 $80000$。 保证所有测试用例中单独电阻器的总数不超过 $320000$。

对于每个测试用例，输出一行： - 如果可以实现等效电阻为 $r$，输出“REVOLTING”，后接 $n$ 个整数 $r_1, r_2, \ldots, r_n$，表示每个电阻器分配的电阻值。这里 $n$ 是电路中的电阻器数量。可能存在多个不同的最优分配方案，你可以输出任意一个； - 如果无法实现，输出字符串“LOSS”。

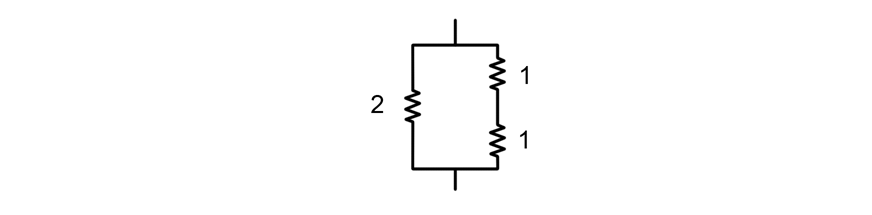
以下是第三个样例的说明：  这里，各电阻器的电阻和为 $2 + 1 + 1 = 4$，可以证明这是最小值。注意，可能存在其他达到该最小值的分配方案。 由 ChatGPT 4.1 翻译