CF1286B Numbers on Tree

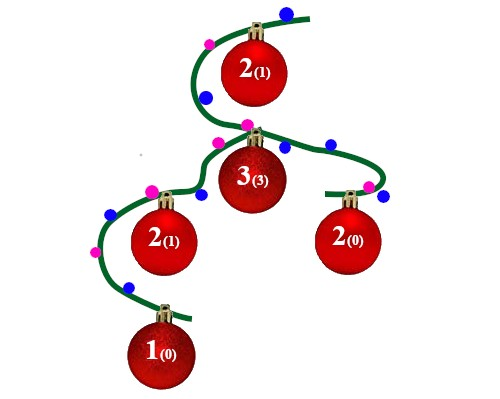
Evlampiy 收到了一棵有根树作为礼物。树的顶点从 $1$ 到 $n$ 编号，每个顶点上都写有一个整数 $a_i$。对于每个顶点 $i$，Evlampiy 计算了 $c_i$ —— 在以顶点 $i$ 为根的子树中，满足 $a_j < a_i$ 的顶点 $j$ 的数量。  上图为第二个样例的说明，顶点上的第一个整数为 $a_i$，括号内的整数为 $c_i$。 新年过后，Evlampiy 忘记了他的礼物是什么！他只记得树的结构和每个顶点的 $c_i$ 值，但完全忘记了每个顶点上写的整数 $a_i$。 请你帮助他还原这些初始的整数！

第一行包含一个整数 $n$ $(1 \leq n \leq 2000)$，表示树的顶点数。 接下来的 $n$ 行描述每个顶点：第 $i$ 行包含两个整数 $p_i$ 和 $c_i$（$0 \leq p_i \leq n$；$0 \leq c_i \leq n-1$），其中 $p_i$ 表示顶点 $i$ 的父节点编号，如果顶点 $i$ 是根节点则 $p_i = 0$，$c_i$ 表示在以顶点 $i$ 为根的子树中，满足 $a_j < a_i$ 的顶点 $j$ 的数量。 保证 $p_i$ 的取值描述了一棵有 $n$ 个顶点的有根树。

如果存在解，第一行输出 "YES"。第二行输出 $n$ 个整数 $a_i$（$1 \leq a_i \leq 10^9$），表示每个顶点上写的整数。如果有多组解，输出任意一组即可。可以证明，如果存在解，则一定存在所有 $a_i$ 均在 $1$ 到 $10^9$ 之间的解。 如果无解，输出 "NO"。

由 ChatGPT 4.1 翻译