CF1286D LCC
题目描述
在 Chillland 建造了一条无限长的 Line Chillland Collider(LCC)。有 $n$ 根管道,坐标分别为 $x_i$,它们都连接在 LCC 上。当实验在时间 $0$ 开始时,第 $i$ 个质子会从第 $i$ 根管道以速度 $v_i$ 飞出。第 $i$ 个质子以概率 $p_i$ 向右飞行,以概率 $1 - p_i$ 向左飞行。实验的持续时间定义为任意两个质子首次碰撞的时间。如果没有发生碰撞,则实验的持续时间视为 $0$。
请你求出实验持续时间的期望值。
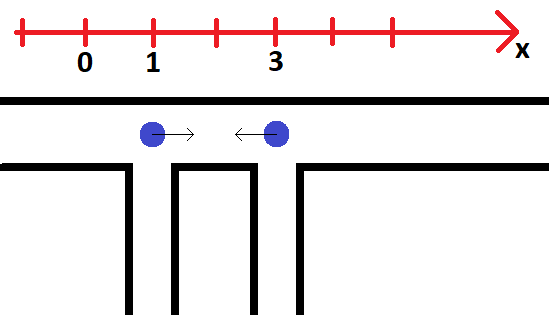 第一组样例的示意图
输入格式
输入的第一行包含一个整数 $n$,表示管道的数量($1 \le n \le 10^5$)。接下来的 $n$ 行,每行包含三个整数 $x_i$、$v_i$、$p_i$,分别表示第 $i$ 根管道的坐标、第 $i$ 个质子的速度,以及第 $i$ 个质子向右飞行的概率(百分比形式)($-10^9 \le x_i \le 10^9, 1 \le v_i \le 10^6, 0 \le p_i \le 100$)。保证所有 $x_i$ 坐标互不相同且递增。
输出格式
可以证明,答案总可以表示为一个分数 $P/Q$,其中 $P$ 是整数,$Q$ 是一个不被 $998\,244\,353$ 整除的正整数。在这种情况下,请输出 $P \cdot Q^{-1}$ 对 $998\,244\,353$ 取模的结果。
说明/提示
由 ChatGPT 4.1 翻译