CF1290B Irreducible Anagrams

我们称两个字符串 $s$ 和 $t$ 互为「变位词」，如果可以通过重新排列字符串 $s$ 中的字符得到与 $t$ 相等的字符串。 现在考虑两个互为变位词的字符串 $s$ 和 $t$。如果存在一个整数 $k \ge 2$，以及 $2k$ 个非空字符串 $s_1, t_1, s_2, t_2, \dots, s_k, t_k$，满足以下条件，则称 $t$ 是 $s$ 的「可约变位词」： 1. 按顺序拼接 $s_1, s_2, \dots, s_k$ 得到的字符串等于 $s$； 2. 按顺序拼接 $t_1, t_2, \dots, t_k$ 得到的字符串等于 $t$； 3. 对于所有 $1 \le i \le k$，$s_i$ 和 $t_i$ 互为变位词。 如果不存在这样的划分，则称 $t$ 是 $s$ 的「不可约变位词」。注意，这些定义仅在 $s$ 和 $t$ 互为变位词时才有意义。 例如，考虑字符串 $s = $ "gamegame"。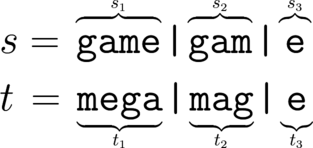则字符串 $t = $ "megamage" 是 $s$ 的可约变位词，例如可以选择 $s_1 = $ "game"，$s_2 = $ "gam"，$s_3 = $ "e"，$t_1 = $ "mega"，$t_2 = $ "mag"，$t_3 = $ "e"：  另一方面，可以证明 $t = $ "memegaga" 是 $s$ 的不可约变位词。 现在给定一个字符串 $s$ 和 $q$ 个询问，每个询问由两个整数 $1 \le l \le r \le |s|$（其中 $|s|$ 表示字符串 $s$ 的长度）组成。对于每个询问，你需要判断 $s$ 的第 $l$ 个字符到第 $r$ 个字符组成的子串，是否存在至少一个不可约变位词。

第一行包含一个仅由小写英文字母组成的字符串 $s$（$1 \le |s| \le 2 \times 10^5$）。 第二行包含一个整数 $q$（$1 \le q \le 10^5$），表示询问的个数。 接下来的 $q$ 行，每行包含两个整数 $l$ 和 $r$（$1 \le l \le r \le |s|$），表示一次询问，询问 $s$ 的第 $l$ 个字符到第 $r$ 个字符组成的子串。

对于每个询问，如果对应的子串存在至少一个不可约变位词，输出一行 "Yes"（不含引号）；否则输出一行 "No"（不含引号）。

在第一个样例中，第一个和第三个询问的子串都是 "a"，它本身就是不可约变位词，因为无法将其划分为两个或更多非空字符串。而第二个询问的子串是 "aaa"，它没有不可约变位词：它唯一的变位词就是它本身，可以选择 $s_1 = $ "a"，$s_2 = $ "aa"，$t_1 = $ "a"，$t_2 = $ "aa"，从而证明它是可约变位词。 在第二个样例的第二个询问中，子串为 "abb"，例如 "bba" 就是它的不可约变位词。 由 ChatGPT 4.1 翻译