CF1290E Cartesian Tree
题目描述
Ildar 是 William 和 Harris 的算法老师。今天,Ildar 正在讲解笛卡尔树。然而,Harris 生病了,所以 Ildar 只教了 William。
笛卡尔树是一种有根树,可以从一组互不相同的整数序列构建。我们按照如下方式构建笛卡尔树:
1. 如果序列为空,返回一棵空树;
2. 设最大元素的位置为 $x$;
3. 从序列中移除位置 $x$ 的元素,并将序列分为左部分和右部分(可能为空)(实际上并不真正移除,只是暂时取出);
4. 分别为左右部分递归构建笛卡尔树;
5. 为位置 $x$ 的元素创建一个新结点,作为新树的根节点。然后,将左部分和右部分的根节点(如果存在)作为该结点的子节点;
6. 返回构建好的树。
例如,序列 $4, 2, 7, 3, 5, 6, 1$ 的笛卡尔树如下所示:
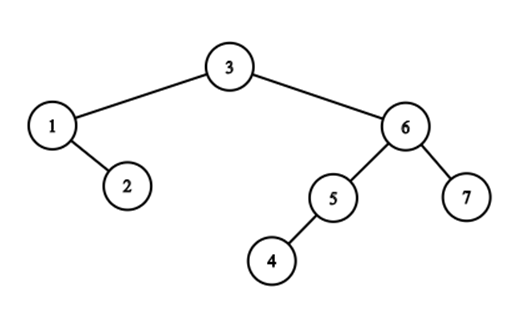
在讲解完笛卡尔树后,Ildar 布置了作业。他从一个空序列 $a$ 开始。
在第 $i$ 轮,他会在 $a$ 的某个位置插入一个值为 $i$ 的元素。然后,他会提出一个问题:当前序列 $a$ 的笛卡尔树中,每个结点的子树大小之和是多少?
如果结点 $v$ 在结点 $u$ 的子树中,当且仅当 $v = u$ 或 $v$ 是 $u$ 某个子节点的子树中的结点。结点 $u$ 的子树大小是满足 $v$ 在 $u$ 的子树中的结点 $v$ 的数量。
Ildar 总共会进行 $n$ 轮。作业就是回答这 $n$ 个问题的答案序列。
第二天,Ildar 告诉 Harris,他也要完成这份作业。Harris 从 William 那里得到了最终的序列 $a$,但他不知道如何求出这 $n$ 个问题的答案。请你帮助 Harris!
输入格式
第一行包含一个整数 $n$($1 \le n \le 150000$)。
第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$($1 \le a_i \le n$)。保证 $1$ 到 $n$ 的每个整数在序列中恰好出现一次。
输出格式
输出 $n$ 行,第 $i$ 行输出一个整数,表示第 $i$ 个问题的答案。
说明/提示
第一轮后,序列为 $1$。树为:

答案是 $1$。
第二轮后,序列为 $2, 1$。树为:
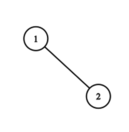
答案是 $2+1=3$。
第三轮后,序列为 $2, 1, 3$。树为:
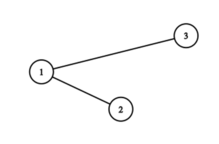
答案是 $2+1+3=6$。
第四轮后,序列为 $2, 4, 1, 3$。树为:
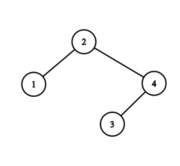
答案是 $1+4+1+2=8$。
第五轮后,序列为 $2, 4, 1, 5, 3$。树为:
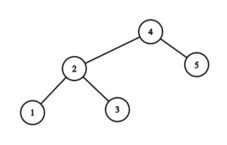
答案是 $1+3+1+5+1=11$。
由 ChatGPT 4.1 翻译