CF1290E Cartesian Tree

Ildar is the algorithm teacher of William and Harris. Today, Ildar is teaching Cartesian Tree. However, Harris is sick, so Ildar is only teaching William. A cartesian tree is a rooted tree, that can be constructed from a sequence of distinct integers. We build the cartesian tree as follows: 1. If the sequence is empty, return an empty tree; 2. Let the position of the maximum element be $ x $ ; 3. Remove element on the position $ x $ from the sequence and break it into the left part and the right part (which might be empty) (not actually removing it, just taking it away temporarily); 4. Build cartesian tree for each part; 5. Create a new vertex for the element, that was on the position $ x $ which will serve as the root of the new tree. Then, for the root of the left part and right part, if exists, will become the children for this vertex; 6. Return the tree we have gotten. 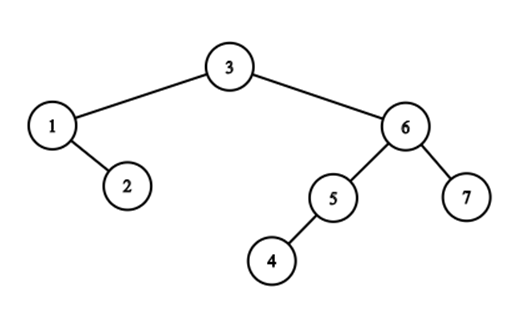For example, this is the cartesian tree for the sequence $ 4, 2, 7, 3, 5, 6, 1 $ : After teaching what the cartesian tree is, Ildar has assigned homework. He starts with an empty sequence $ a $ . In the $ i $ -th round, he inserts an element with value $ i $ somewhere in $ a $ . Then, he asks a question: what is the sum of the sizes of the subtrees for every node in the cartesian tree for the current sequence $ a $ ? Node $ v $ is in the node $ u $ subtree if and only if $ v = u $ or $ v $ is in the subtree of one of the vertex $ u $ children. The size of the subtree of node $ u $ is the number of nodes $ v $ such that $ v $ is in the subtree of $ u $ . Ildar will do $ n $ rounds in total. The homework is the sequence of answers to the $ n $ questions. The next day, Ildar told Harris that he has to complete the homework as well. Harris obtained the final state of the sequence $ a $ from William. However, he has no idea how to find the answers to the $ n $ questions. Help Harris!

The first line contains a single integer $ n $ ( $ 1 \le n \le 150000 $ ). The second line contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ 1 \le a_i \le n $ ). It is guarenteed that each integer from $ 1 $ to $ n $ appears in the sequence exactly once.

Print $ n $ lines, $ i $ -th line should contain a single integer — the answer to the $ i $ -th question.

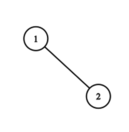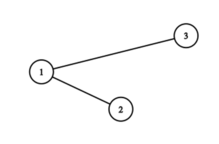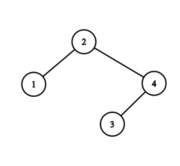After the first round, the sequence is $ 1 $ . The tree is The answer is $ 1 $ . After the second round, the sequence is $ 2, 1 $ . The tree is The answer is $ 2+1=3 $ . After the third round, the sequence is $ 2, 1, 3 $ . The tree is The answer is $ 2+1+3=6 $ . After the fourth round, the sequence is $ 2, 4, 1, 3 $ . The tree is The answer is $ 1+4+1+2=8 $ . After the fifth round, the sequence is $ 2, 4, 1, 5, 3 $ . 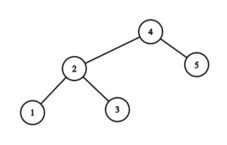The tree is The answer is $ 1+3+1+5+1=11 $ .