CF1290F Making Shapes
题目描述
给定 $n$ 个两两不共线的二维向量。你可以用以下方式在二维平面上用这些向量构造图形:
1. 从原点 $(0, 0)$ 开始。
2. 选择一个向量,将该向量的线段加到当前点。例如,如果当前点在 $(x, y)$,你选择向量 $(u, v)$,则从当前点画一条线段到 $(x + u, y + v)$,并将当前点更新为 $(x + u, y + v)$。
3. 重复第 2 步,直到你再次回到原点。
每个向量可以重复使用任意多次。
请计算可以用上述步骤构造出的不同的、非退化(面积大于 $0$)且凸的图形的数量,要求这些图形的构成向量按逆时针顺序排列,并且该图形可以通过平移被包含在一个 $m \times m$ 的正方形内。由于答案可能很大,请对 $998244353$ 取模。
如果存在某种平行移动能使第一个图形与第二个图形重合,则认为这两个图形是相同的。
如果存在某种平行移动,使得图形内或边界上的每个点 $(u, v)$ 都满足 $0 \leq u, v \leq m$,则认为该图形可以被包含在 $m \times m$ 的正方形内。
输入格式
第一行包含两个整数 $n$ 和 $m$,分别表示向量的数量和正方形的边长($1 \leq n \leq 5$,$1 \leq m \leq 10^9$)。
接下来的 $n$ 行,每行包含两个整数 $x_i$ 和 $y_i$,表示第 $i$ 个向量的 $x$ 坐标和 $y$ 坐标($|x_i|, |y_i| \leq 4$,$(x_i, y_i) \neq (0, 0)$)。
保证任意两个向量都不平行,即对于任意 $1 \leq i < j \leq n$,不存在实数 $k$ 使得 $x_i \cdot k = x_j$ 且 $y_i \cdot k = y_j$。
输出格式
输出一个整数,表示满足条件的图形数量,对 $998244353$ 取模。
说明/提示
第一个样例的所有图形如下:
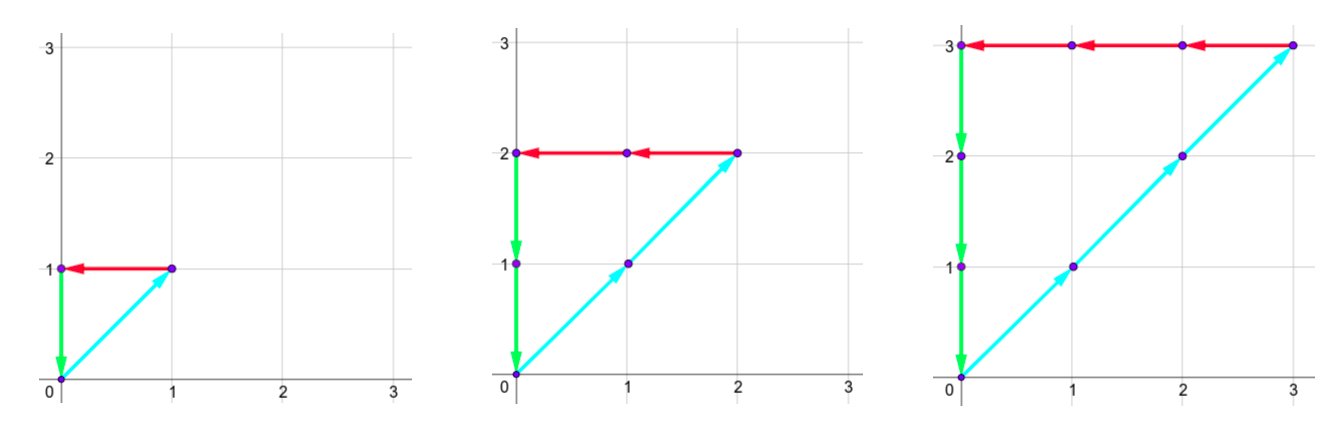
第二个样例的唯一图形如下:
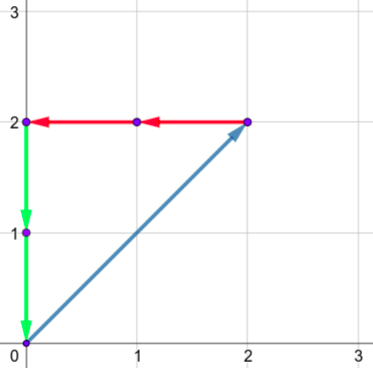
第四个样例的唯一图形如下:
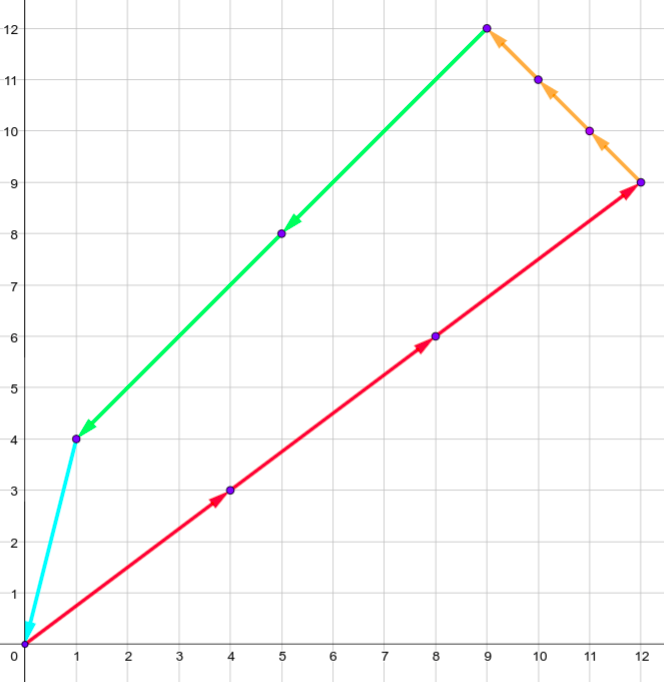
由 ChatGPT 4.1 翻译