CF1292D Chaotic V.

设 $x$ 是大于 $1$ 的正整数，定义 $f(x)$ 为 $x$ 的最小质因子的值。 现在考虑构造一棵树 $T$。其中节点均用从 $1$ 开始的正整数编号，对于任意大于 $1$ 的正整数 $x$，节点 $x$ 在树上的父亲是 $\frac{x}{f(x)}$。 在这棵树上有 $n$ 个关键节点，很特别地，这 $n$ 个节点的编号均可以表示成一个非负整数的阶乘。更具体地，第 $i$ 个节点 $P_i$ 的编号为 $k_i!=\prod_{j=1}^{k_i}j$。 定义 $\text{DIS}(i,j)$ 表示树上 $i,j$ 两点间最短路所包含的边数。现在你找出树上的一个节点 $P$，最小化 $\sum_{i=1}^n\text{DIS}(P,P_i)$ 的值。你只需要输出这个最小值即可。

第一行一个正整数 $n(1\leq n\leq 10^6)$，代表节点数。 第二行 $n$个非负整数 $k_i(0\leq k_i\leq 5\times 10^3)$，描述节点 $P_i$ 的编号为 $k_i!$。

一行一个非负整数表示答案。

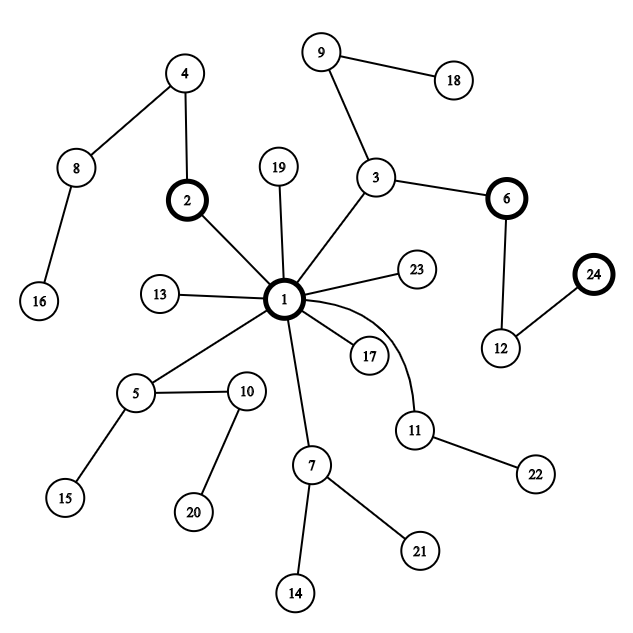
Considering the first $ 24 $ nodes of the system, the node network will look as follows (the nodes $ 1! $ , $ 2! $ , $ 3! $ , $ 4! $ are drawn bold):  For the first example, Ivy will place the emotion samples at the node $ 1 $ . From here: - The distance from Vanessa's first fragment to the node $ 1 $ is $ 1 $ . - The distance from Vanessa's second fragment to the node $ 1 $ is $ 0 $ . - The distance from Vanessa's third fragment to the node $ 1 $ is $ 4 $ . The total length is $ 5 $ . For the second example, the assembly node will be $ 6 $ . From here: - The distance from Vanessa's first fragment to the node $ 6 $ is $ 0 $ . - The distance from Vanessa's second fragment to the node $ 6 $ is $ 2 $ . - The distance from Vanessa's third fragment to the node $ 6 $ is $ 2 $ . - The distance from Vanessa's fourth fragment to the node $ 6 $ is again $ 2 $ . The total path length is $ 6 $ .