CF1294E Obtain a Permutation

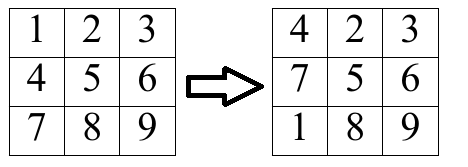
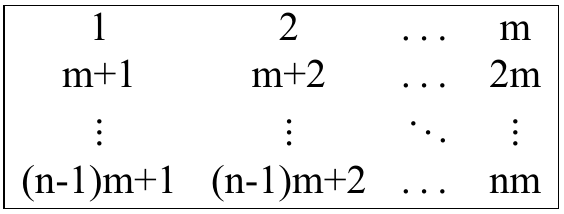
给定一个大小为 $n \times m$ 的矩阵，矩阵中的元素均为 $1$ 到 $2 \cdot 10^5$ 之间的整数。 每次操作，你可以： - 选择矩阵中的任意一个元素，将其值更改为 $1$ 到 $n \cdot m$ 之间的任意整数（包含两端）； - 选择任意一列，将该列进行一次循环上移（见下方示例）。 循环上移操作是指，选择某一列 $j$（$1 \le j \le m$），同时将 $a_{1, j} := a_{2, j}, a_{2, j} := a_{3, j}, \dots, a_{n, j} := a_{1, j}$。  你希望通过最少的操作次数，将矩阵变为如下形式：  换句话说，目标是得到一个矩阵，使得 $a_{1, 1} = 1, a_{1, 2} = 2, \dots, a_{1, m} = m, a_{2, 1} = m + 1, a_{2, 2} = m + 2, \dots, a_{n, m} = n \cdot m$，即 $a_{i, j} = (i - 1) \cdot m + j$，并且操作次数最少。

输入的第一行包含两个整数 $n$ 和 $m$（$1 \le n, m \le 2 \cdot 10^5, n \cdot m \le 2 \cdot 10^5$），表示矩阵的大小。 接下来的 $n$ 行，每行包含 $m$ 个整数，第 $i$ 行第 $j$ 个数为 $a_{i, j}$（$1 \le a_{i, j} \le 2 \cdot 10^5$）。

输出一个整数，表示将矩阵变为目标矩阵所需的最小操作次数。

在第一个样例中，你可以将 $a_{1, 1} := 7, a_{1, 2} := 8, a_{1, 3} := 9$，然后分别对第一、第二、第三列进行一次循环上移，因此答案为 $6$。可以证明无法得到更优的答案。 在第二个样例中，矩阵已经符合要求，因此答案为 $0$。 在第三个样例中，只需对第二列循环上移两次即可得到目标矩阵，因此答案为 $2$。 由 ChatGPT 4.1 翻译