CF1294F Three Paths on a Tree
题目描述
给定一棵有 $n$ 个顶点的无权树。回忆一下,树是一种无环连通无向图。
你的任务是从这棵树上选择三个不同的顶点 $a, b, c$,使得属于 $a$ 和 $b$、$b$ 和 $c$、$a$ 和 $c$ 这三条简单路径中至少一条的边的数量最大。具体可以参考题目下方的说明部分。
简单路径指的是每个顶点最多只访问一次的路径。
输入格式
第一行包含一个整数 $n$($3 \le n \le 2 \cdot 10^5$),表示树的顶点数。
接下来的 $n-1$ 行,每行包含两个整数 $a_i, b_i$($1 \le a_i, b_i \le n$,$a_i \ne b_i$),表示树中的一条边。
保证给定的图是一棵树。
输出格式
第一行输出一个整数 $res$,表示属于 $a$ 和 $b$、$b$ 和 $c$、$a$ 和 $c$ 这三条简单路径中至少一条的边的最大数量。
第二行输出三个整数 $a, b, c$,满足 $1 \le a, b, c \le n$ 且 $a \ne b, b \ne c, a \ne c$。
如果有多组答案,输出任意一组均可。
说明/提示
下图对应第一个样例(以及另一组正确答案):
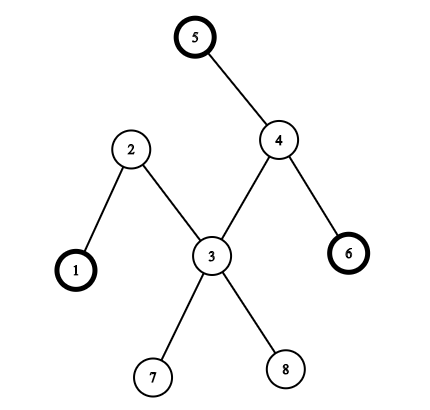
如果选择顶点 $1, 5, 6$,那么 $1$ 到 $5$ 的路径包含边 $(1, 2), (2, 3), (3, 4), (4, 5)$,$1$ 到 $6$ 的路径包含边 $(1, 2), (2, 3), (3, 4), (4, 6)$,$5$ 到 $6$ 的路径包含边 $(4, 5), (4, 6)$。这三条路径的并集为 $(1, 2), (2, 3), (3, 4), (4, 5), (4, 6)$,所以答案是 $5$。可以证明不存在更优的答案。
由 ChatGPT 4.1 翻译