CF1294F Three Paths on a Tree

You are given an unweighted tree with $ n $ vertices. Recall that a tree is a connected undirected graph without cycles. Your task is to choose three distinct vertices $ a, b, c $ on this tree such that the number of edges which belong to at least one of the simple paths between $ a $ and $ b $ , $ b $ and $ c $ , or $ a $ and $ c $ is the maximum possible. See the notes section for a better understanding. The simple path is the path that visits each vertex at most once.

The first line contains one integer number $ n $ ( $ 3 \le n \le 2 \cdot 10^5 $ ) — the number of vertices in the tree. Next $ n - 1 $ lines describe the edges of the tree in form $ a_i, b_i $ ( $ 1 \le a_i $ , $ b_i \le n $ , $ a_i \ne b_i $ ). It is guaranteed that given graph is a tree.

In the first line print one integer $ res $ — the maximum number of edges which belong to at least one of the simple paths between $ a $ and $ b $ , $ b $ and $ c $ , or $ a $ and $ c $ . In the second line print three integers $ a, b, c $ such that $ 1 \le a, b, c \le n $ and $ a \ne, b \ne c, a \ne c $ . If there are several answers, you can print any.

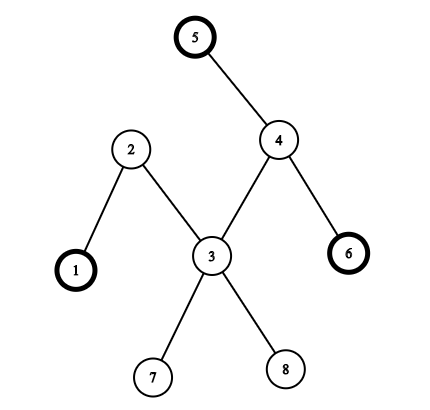
The picture corresponding to the first example (and another one correct answer):  If you choose vertices $ 1, 5, 6 $ then the path between $ 1 $ and $ 5 $ consists of edges $ (1, 2), (2, 3), (3, 4), (4, 5) $ , the path between $ 1 $ and $ 6 $ consists of edges $ (1, 2), (2, 3), (3, 4), (4, 6) $ and the path between $ 5 $ and $ 6 $ consists of edges $ (4, 5), (4, 6) $ . The union of these paths is $ (1, 2), (2, 3), (3, 4), (4, 5), (4, 6) $ so the answer is $ 5 $ . It can be shown that there is no better answer.