CF1299D Around the World

Guy-Manuel 和 Thomas 正在计划 $144$ 次环游世界的旅行。 给定一个简单的带权无向连通图，包含 $n$ 个顶点和 $m$ 条边，满足以下限制：不存在任何长度大于 $3$ 的简单环（即不经过任何顶点超过一次的环）经过顶点 $1$。一条路径（不一定是简单路径）的代价定义为该路径上所有边的权值的 [异或](https://en.wikipedia.org/wiki/Bitwise_operation#XOR)（每条边经过几次就计几次）。 但代价为 $0$ 的旅行并不令人兴奋。 你可以选择任意一组与顶点 $1$ 相连的边，并将它们删除。请问有多少种选择方式，使得删除后，图中不存在任何经过顶点 $1$ 的、代价为 $0$ 的非平凡环？一个环被称为非平凡环，当且仅当它经过某条边奇数次。由于答案可能很大，请输出对 $10^9+7$ 取模的结果。

第一行包含两个整数 $n$ 和 $m$（$1 \le n,m \le 10^5$），表示图中顶点和边的数量。接下来的 $m$ 行，每行包含三个整数 $a_i$、$b_i$ 和 $w_i$（$1 \le a_i, b_i \le n, a_i \neq b_i, 0 \le w_i < 32$），表示第 $i$ 条边的两个端点和权值。保证不存在重边，图是连通的，且不存在长度大于 $3$ 的简单环经过顶点 $1$。

输出满足条件的方案数，对 $10^9+7$ 取模。

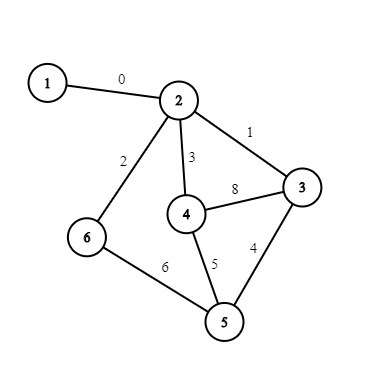
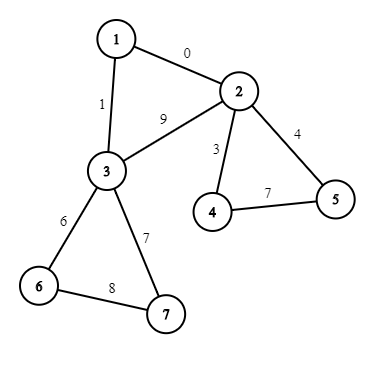
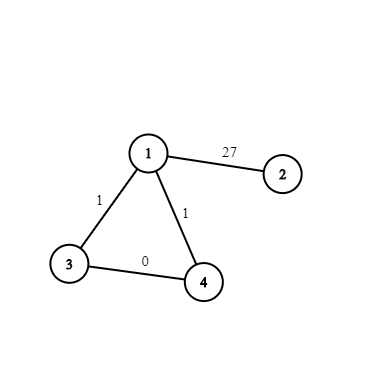
下图展示了样例中的图。  在第一个样例中，不存在任何代价为 $0$ 的非平凡环，因此我们可以选择删除或保留唯一一条与顶点 $1$ 相连的边。  在第二个样例中，如果不删除边 $1-2$，则存在一个代价为 $0$ 的环 $1-2-4-5-2-1$；同理，如果不删除边 $1-3$，则存在一个代价为 $0$ 的环 $1-3-2-4-5-2-3-1$。唯一合法的选择是同时删除这两条边。  在第三个样例中，所有的选择都是合法的，除了同时保留 $1-3$ 和 $1-4$ 这两条边的情况。 由 ChatGPT 4.1 翻译