CF1304E 1-Trees and Queries

Gildong was hiking a mountain, walking by millions of trees. Inspired by them, he suddenly came up with an interesting idea for trees in data structures: What if we add another edge in a tree? Then he found that such tree-like graphs are called 1-trees. Since Gildong was bored of solving too many tree problems, he wanted to see if similar techniques in trees can be used in 1-trees as well. Instead of solving it by himself, he's going to test you by providing queries on 1-trees. First, he'll provide you a tree (not 1-tree) with $ n $ vertices, then he will ask you $ q $ queries. Each query contains $ 5 $ integers: $ x $ , $ y $ , $ a $ , $ b $ , and $ k $ . This means you're asked to determine if there exists a path from vertex $ a $ to $ b $ that contains exactly $ k $ edges after adding a bidirectional edge between vertices $ x $ and $ y $ . A path can contain the same vertices and same edges multiple times. All queries are independent of each other; i.e. the added edge in a query is removed in the next query.

The first line contains an integer $ n $ ( $ 3 \le n \le 10^5 $ ), the number of vertices of the tree. Next $ n-1 $ lines contain two integers $ u $ and $ v $ ( $ 1 \le u,v \le n $ , $ u \ne v $ ) each, which means there is an edge between vertex $ u $ and $ v $ . All edges are bidirectional and distinct. Next line contains an integer $ q $ ( $ 1 \le q \le 10^5 $ ), the number of queries Gildong wants to ask. Next $ q $ lines contain five integers $ x $ , $ y $ , $ a $ , $ b $ , and $ k $ each ( $ 1 \le x,y,a,b \le n $ , $ x \ne y $ , $ 1 \le k \le 10^9 $ ) – the integers explained in the description. It is guaranteed that the edge between $ x $ and $ y $ does not exist in the original tree.

For each query, print "YES" if there exists a path that contains exactly $ k $ edges from vertex $ a $ to $ b $ after adding an edge between vertices $ x $ and $ y $ . Otherwise, print "NO". You can print each letter in any case (upper or lower).

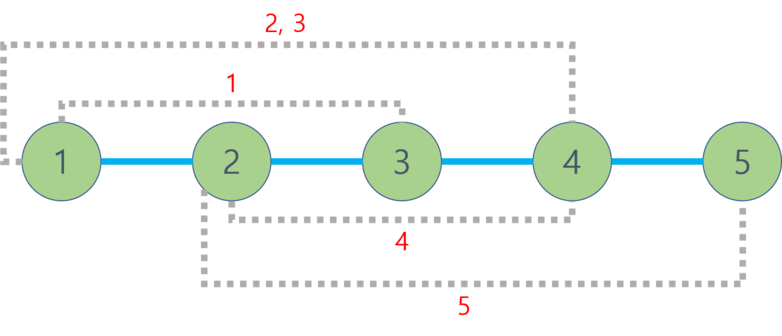The image below describes the tree (circles and solid lines) and the added edges for each query (dotted lines). Possible paths for the queries with "YES" answers are: - $ 1 $ -st query: $ 1 $ – $ 3 $ – $ 2 $ - $ 2 $ -nd query: $ 1 $ – $ 2 $ – $ 3 $ - $ 4 $ -th query: $ 3 $ – $ 4 $ – $ 2 $ – $ 3 $ – $ 4 $ – $ 2 $ – $ 3 $ – $ 4 $ – $ 2 $ – $ 3 $