CF1307F Cow and Vacation

Bessie 正在准备度假。 她所在的加利奶牛亚洲有 $n$ 个城市，$n-1$ 条双向道路连接。保证可以从任意一个城市到任意一个城市。 Bessie 考虑了 $v$ 种度假方案，每种方案包括从城市 $a_i$ 开始到城市 $b_i$ 结束。 已知一共有 $r$ 个城市拥有休息点。Bessie 容易疲倦，并且她不能在不休息的情况下穿越超过 $k$ 条连续道路。有时，她还会为了休息而多次穿过同一个城市。 对于每一种旅行方案，Bessie 是否有从出发城市到结束地城市的旅行方式？

第一行包括三个整数，$n,k,r$（$2\le n\le2\times10^5$，$1\le k,r\le n$）。分别表示城市的数量，Bessie 愿意在不休息的情况下连续通过的最大道路数，休息点的数量。 接下来 $n-1$ 行，每行两个整数写 $x_i$ 和 $y_i$（$1\le x_i,y_i\le n$，$x_i\ne y_i$），表示从 $x_i$ 到 $y_i$ 有一条双向道路连接。 接下来 $r$ 行，每行一个数字，表示有休息点的城市，保证每个城市最多出现一遍。 接下来一行一个整数 $v$（$1\le v\le2\times10^5$），表示度假方案数。 接下来 $v$ 行，每行两个整数 $a_i$ 和 $b_i$（$1\le a_i,b_i\le n$，$a_i\ne b_i$），表示该方案从 $a_i$ 开始到城市 $b_i$ 结束。

一共 $v$ 行，表示如果 Bessie 能够按要求到达，输出 `YES`，反之输出 `NO`。

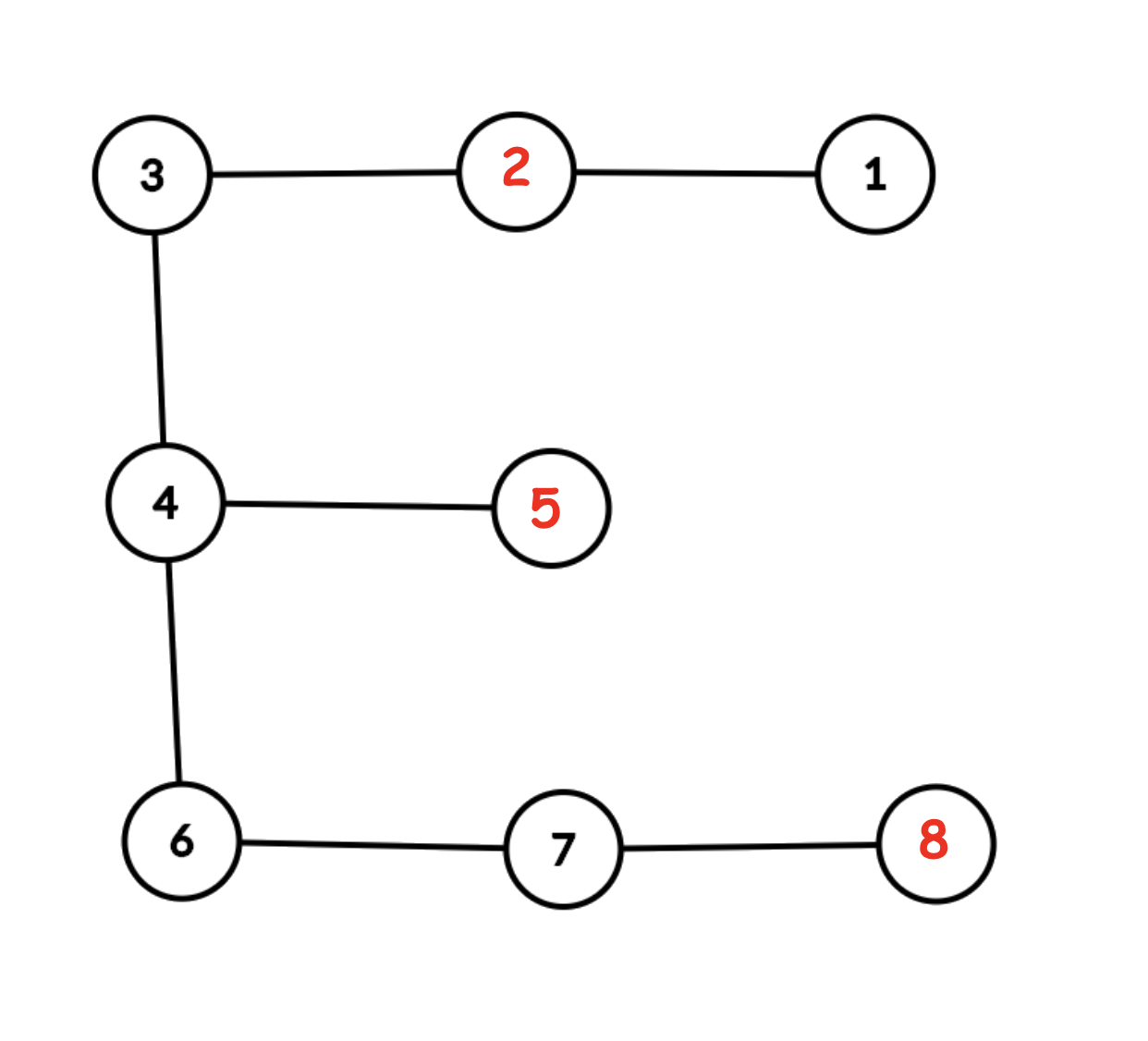
第一个例子的图表如下所示。休息站用红色表示。 对于第一个查询，Bessie 可以按以下顺序访问这些城市：$1,2,3$。 对于第二个查询，Bessie 可以按以下顺序访问这些城市：$3,2,4,5$。 对于第三个查询，Bessie 无法前往目的地。例如，如果她试图这样旅行：$3,2,4,5,6$，她在两条以上的道路上旅行而没有休息。  第二个样例的图如下。