CF1310B Double Elimination

一年一度的盛事——Cota 2 世界锦标赛“The Innernational”即将拉开帷幕。共有 $2^n$ 支队伍将以双败淘汰制（即使你了解该赛制，也请仔细阅读题目描述）争夺冠军。 队伍编号为 $1$ 到 $2^n$，比赛为一对一对决。所有队伍均从胜者组开始。 胜者组的比赛将在尚未输过任何比赛的队伍之间进行。队伍按编号分组进行比赛，获胜者晋级胜者组下一轮，失败者则进入败者组。 败者组从第一轮胜者组中落败的 $2^{n-1}$ 支队伍开始。每一轮败者组包含两场比赛。该轮的第一场比赛中，$2^k$ 支队伍两两对决（队伍按编号分组）。$2^{k-1}$ 支失败队伍被淘汰，$2^{k-1}$ 支获胜队伍将与本轮胜者组被淘汰的 $2^{k-1}$ 支队伍进行比赛（同样按编号分组）。每一轮结束后，胜者组和败者组各剩下 $2^{k-1}$ 支队伍。具体可参考样例说明。 最终，胜者组仅剩的一支队伍将与败者组仅剩的一支队伍在总决赛中争夺冠军。 你是编号为 $a_1, a_2, ..., a_k$ 的队伍的粉丝。你希望锦标赛中包含你喜欢的队伍的比赛尽可能多。幸运的是，你可以随意操控每场比赛的结果。请问，最多能有多少场包含你喜欢队伍的比赛？

第一行包含两个整数 $n, k$，表示共有 $2^n$ 支队伍参加锦标赛，你是 $k$ 支队伍的粉丝（$2 \le n \le 17; 0 \le k \le 2^n$）。 第二行包含 $k$ 个互不相同的整数 $a_1, \ldots, a_k$，表示你喜欢的队伍的编号（$1 \le a_i \le 2^n$）。

输出一个整数，表示最多能有多少场包含你喜欢队伍的比赛。

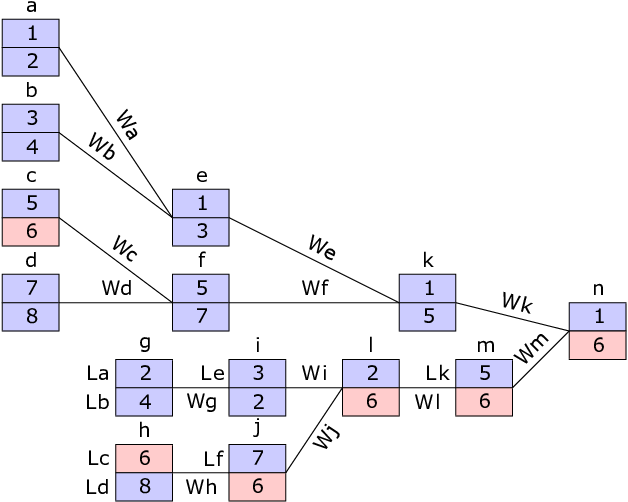
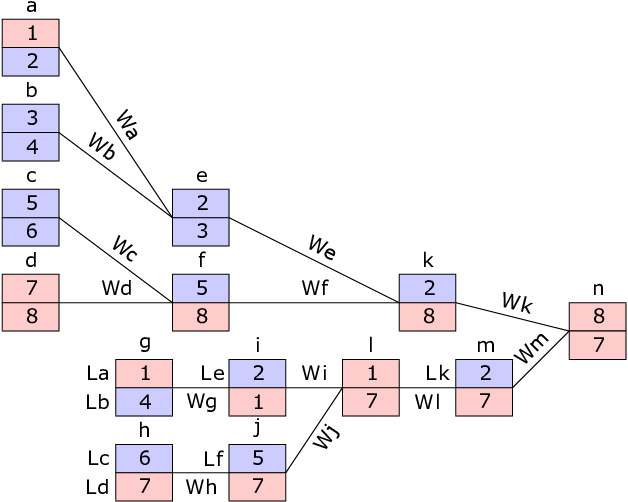
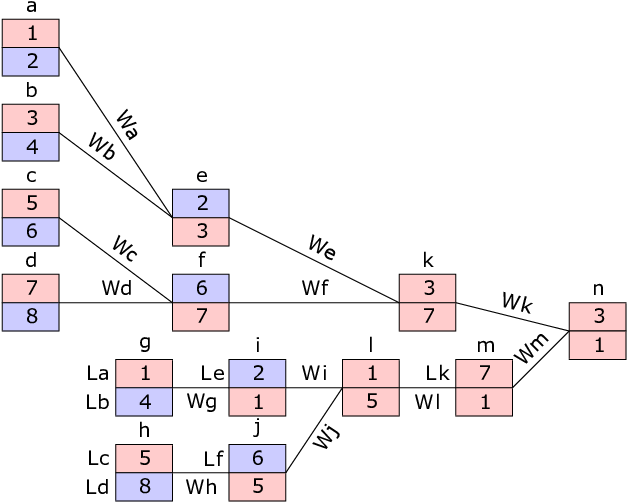
在下图中，锦标赛的每场比赛用英文字母（$a$ 到 $n$）表示。第 $i$ 场比赛的胜者记为 $Wi$，败者记为 $Li$。你喜欢的队伍用红色高亮显示。 在第一个样例中，如果队伍 $6$ 在首轮胜者组比赛（比赛 $c$）中落败，并在之后的所有败者组比赛（比赛 $h, j, l, m$）中获胜，则它将参加 6 场比赛。  在第二个样例中，队伍 $7$ 和 $8$ 必须在胜者组首轮（比赛 $d$）中相遇。队伍 $8$ 可以赢下胜者组剩余所有比赛，而队伍 $1$ 和 $7$ 则在败者组中竞争。  在第三个样例中，你喜欢的队伍可以参加锦标赛的所有比赛。  由 ChatGPT 4.1 翻译