CF1311E Construct the Binary Tree

You are given two integers $ n $ and $ d $ . You need to construct a rooted binary tree consisting of $ n $ vertices with a root at the vertex $ 1 $ and the sum of depths of all vertices equals to $ d $ . A tree is a connected graph without cycles. A rooted tree has a special vertex called the root. A parent of a vertex $ v $ is the last different from $ v $ vertex on the path from the root to the vertex $ v $ . The depth of the vertex $ v $ is the length of the path from the root to the vertex $ v $ . Children of vertex $ v $ are all vertices for which $ v $ is the parent. The binary tree is such a tree that no vertex has more than $ 2 $ children. You have to answer $ t $ independent test cases.

The first line of the input contains one integer $ t $ ( $ 1 \le t \le 1000 $ ) — the number of test cases. The only line of each test case contains two integers $ n $ and $ d $ ( $ 2 \le n, d \le 5000 $ ) — the number of vertices in the tree and the required sum of depths of all vertices. It is guaranteed that the sum of $ n $ and the sum of $ d $ both does not exceed $ 5000 $ ( $ \sum n \le 5000, \sum d \le 5000 $ ).

For each test case, print the answer. If it is impossible to construct such a tree, print "NO" (without quotes) in the first line. Otherwise, print "{YES}" in the first line. Then print $ n-1 $ integers $ p_2, p_3, \dots, p_n $ in the second line, where $ p_i $ is the parent of the vertex $ i $ . Note that the sequence of parents you print should describe some binary tree.

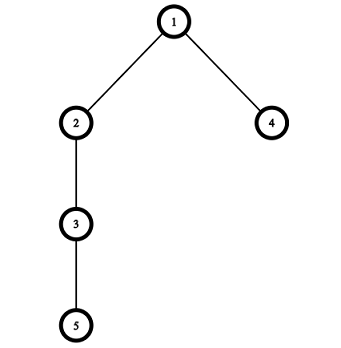
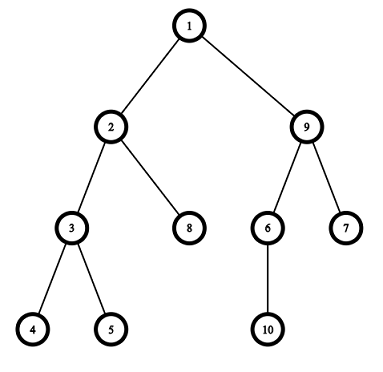
Pictures corresponding to the first and the second test cases of the example: