Different Rules

## 题意简述 一项奥林匹克竞赛有着与普通竞赛不同的规则，它分成两轮，假如一位参赛者在第一轮中排名第 $x$ 名，在第二轮中排名第 $y$ 名，则他的总分是 $x+y$，他的总排名是总分小于等于 $x+y$ 的参赛者（包括他自己）。需要注意的是，每一轮比赛都不会出现并列的情况，每一个排名 $i$ 都对应了唯一的参赛者。 尼古拉被告知他第一轮排名第 $x$ ，第二轮排名第 $y$ ，他需要你帮助他算出他可能获得的最好总排名和最差总排名 ## 输入格式 第一行一个整数 $t(1≤t≤100)$,表示有 $t$ 组测试数据 以下 $t$ 行每行三个整数 $n,x,y(1≤n≤10^9,1≤x,y≤n)$ 表示有 $n$ 名参赛者，尼古拉在第一轮和第二轮分别排名 $x,y$ ## 输出格式 共 $t$ 行，每行两个整数，尼古拉可能获得的的最好总排名和最差总排名

Nikolay has only recently started in competitive programming, but already qualified to the finals of one prestigious olympiad. There going to be $ n $ participants, one of whom is Nikolay. Like any good olympiad, it consists of two rounds. Tired of the traditional rules, in which the participant who solved the largest number of problems wins, the organizers came up with different rules. Suppose in the first round participant A took $ x $ -th place and in the second round — $ y $ -th place. Then the total score of the participant A is sum $ x + y $ . The overall place of the participant A is the number of participants (including A) having their total score less than or equal to the total score of A. Note, that some participants may end up having a common overall place. It is also important to note, that in both the first and the second round there were no two participants tying at a common place. In other words, for every $ i $ from $ 1 $ to $ n $ exactly one participant took $ i $ -th place in first round and exactly one participant took $ i $ -th place in second round. Right after the end of the Olympiad, Nikolay was informed that he got $ x $ -th place in first round and $ y $ -th place in the second round. Nikolay doesn't know the results of other participants, yet he wonders what is the minimum and maximum place he can take, if we consider the most favorable and unfavorable outcome for him. Please help Nikolay to find the answer to this question.

The first line contains an integer $ t $ ( $ 1 \le t \le 100 $ ) — the number of test cases to solve. Each of the following $ t $ lines contains integers $ n $ , $ x $ , $ y $ ( $ 1 \leq n \leq 10^9 $ , $ 1 \le x, y \le n $ ) — the number of participants in the olympiad, the place that Nikolay took in the first round and the place that Nikolay took in the second round.

Print two integers — the minimum and maximum possible overall place Nikolay could take.

1
5 1 3

1 3

1
6 3 4

2 6

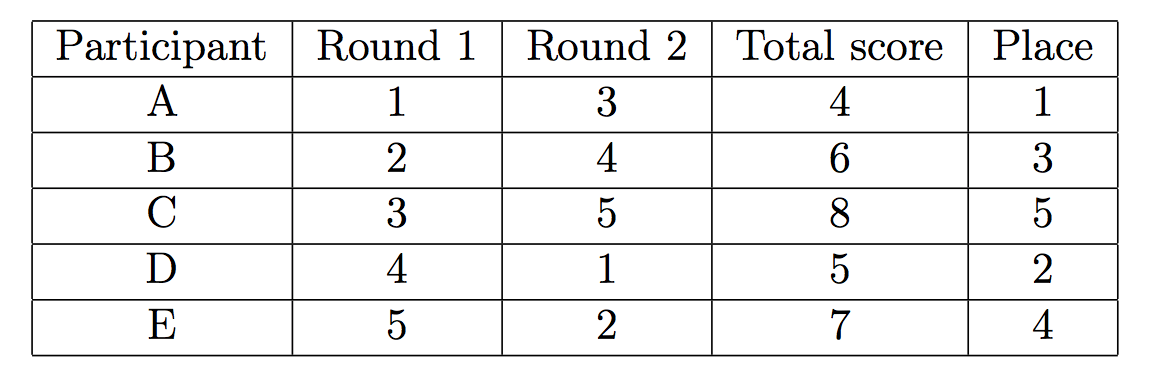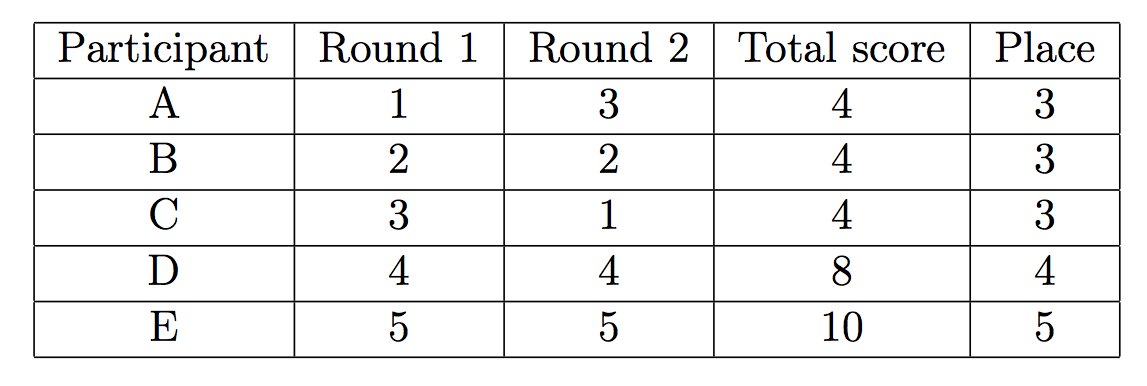Explanation for the first example: Suppose there were 5 participants A-E. Let's denote Nikolay as A. The the most favorable results for Nikolay could look as follows: However, the results of the Olympiad could also look like this: In the first case Nikolay would have taken first place, and in the second — third place.