CF1323B Count Subrectangles

给定一个长度为 $n$ 的数组 $a$ 和一个长度为 $m$ 的数组 $b$，它们的元素均为 $0$ 或 $1$。定义一个 $n \times m$ 的矩阵 $c$，其中 $c_{i, j} = a_i \cdot b_j$（即 $a_i$ 与 $b_j$ 的乘积）。显然，$c$ 也只包含 $0$ 和 $1$。 请问，在矩阵 $c$ 中，面积为 $k$ 且全部元素均为 $1$ 的子矩形有多少个？ 一个子矩形是指若干连续行与若干连续列的交集。即，给定四个整数 $x_1, x_2, y_1, y_2$（$1 \le x_1 \le x_2 \le n$，$1 \le y_1 \le y_2 \le m$），子矩形 $c[x_1 \dots x_2][y_1 \dots y_2]$ 表示第 $x_1$ 行到第 $x_2$ 行与第 $y_1$ 列到第 $y_2$ 列的交集。 子矩形的面积即为其包含的单元格总数。

第一行包含三个整数 $n$、$m$ 和 $k$（$1 \leq n, m \leq 40\,000, 1 \leq k \leq n \cdot m$），分别表示数组 $a$ 的长度、数组 $b$ 的长度和所需子矩形的面积。 第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$0 \leq a_i \leq 1$），表示数组 $a$ 的元素。 第三行包含 $m$ 个整数 $b_1, b_2, \ldots, b_m$（$0 \leq b_i \leq 1$），表示数组 $b$ 的元素。

输出一个整数，表示在矩阵 $c$ 中，面积为 $k$ 且全部元素均为 $1$ 的子矩形的个数。

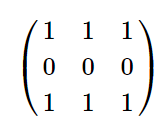
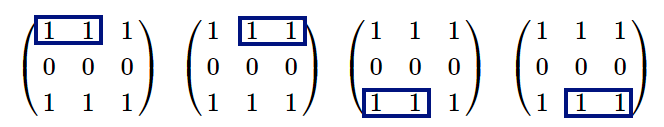
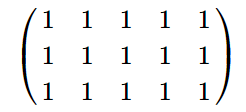
在第一个样例中，矩阵 $c$ 如下：  其中，面积为 $2$ 且全部为 $1$ 的子矩形共有 $4$ 个：  在第二个样例中，矩阵 $c$ 如下：  由 ChatGPT 4.1 翻译