CF1324C Frog Jumps

有一只青蛙停留在字符串 $s = s_1 s_2 \ldots s_n$ 的左侧（更准确地说，青蛙最初位于第 $0$ 号格子）。字符串 $s$ 由 $n$ 个字符组成，每个字符都是 'L' 或 'R'。这意味着，如果青蛙停在第 $i$ 个格子且第 $i$ 个字符为 'L'，青蛙只能向左跳；如果青蛙停在第 $i$ 个格子且第 $i$ 个字符为 'R'，青蛙只能向右跳。青蛙只能从第 $0$ 号格子向右跳。 注意，青蛙可以多次跳到同一个格子，并且可以进行任意多次跳跃。 青蛙希望到达第 $n+1$ 号格子。青蛙在第一次跳跃前会选择一个正整数 $d$（之后不能更改），每次跳跃最多可以跳 $d$ 个格子。也就是说，如果第 $i$ 个字符为 'L'，青蛙可以跳到区间 $[\max(0, i-d), i-1]$ 内的任意格子；如果第 $i$ 个字符为 'R'，青蛙可以跳到区间 $[i+1, \min(n+1, i+d)]$ 内的任意格子。 青蛙不想跳得太远，所以你的任务是求出最小的 $d$，使得青蛙能够从 $0$ 号格子跳到 $n+1$ 号格子，并且每次跳跃不超过 $d$ 个格子。保证一定存在一种方案可以从 $0$ 跳到 $n+1$。 你需要回答 $t$ 组独立的测试用例。

输入的第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。 接下来的 $t$ 行，每行描述一个测试用例。第 $i$ 个测试用例为一个字符串 $s$，长度至少为 $1$，至多为 $2 \cdot 10^5$，只包含字符 'L' 和 'R'。 保证所有测试用例的字符串长度之和不超过 $2 \cdot 10^5$（$\sum |s| \le 2 \cdot 10^5$）。

对于每个测试用例，输出一个答案——即青蛙每次跳跃不超过 $d$ 个格子的情况下，能够从 $0$ 号格子跳到 $n+1$ 号格子的最小 $d$。

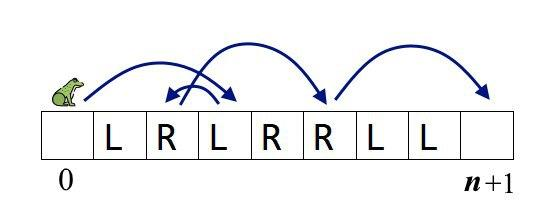
下图描述了第一个样例测试用例及其中一种可能的跳跃方式：  在第二个样例中，青蛙只能直接从 $0$ 跳到 $n+1$。 在第三个样例中，青蛙可以选择 $d=3$，从 $0$ 跳到 $3$，再从 $3$ 跳到 $4$。 在第四个样例中，青蛙可以选择 $d=1$，连续向右跳 $5$ 次。 在第五个样例中，青蛙只能直接从 $0$ 跳到 $n+1$。 在第六个样例中，青蛙可以选择 $d=1$，连续向右跳 $2$ 次。 由 ChatGPT 4.1 翻译