CF1325C Ehab and Path-etic MEXs

给定一棵包含 $n$ 个节点的树。你需要在树的每条边上写上一个标签，使得满足以下条件： - 每个标签都是 $0$ 到 $n-2$ 之间的整数（包含 $0$ 和 $n-2$）。 - 所有标签互不相同。 - 对于所有节点对 $(u,v)$，路径上未出现的最小非负整数 $MEX(u,v)$ 的最大值尽可能小。 这里，$MEX(u,v)$ 表示从节点 $u$ 到节点 $v$ 的唯一路径上未出现的最小非负整数。

第一行包含一个整数 $n$（$2 \le n \le 10^5$），表示树的节点数。 接下来的 $n-1$ 行，每行包含两个用空格分隔的整数 $u$ 和 $v$（$1 \le u,v \le n$），表示节点 $u$ 和节点 $v$ 之间有一条边。保证输入的图是一棵树。

输出 $n-1$ 个整数，第 $i$ 个整数表示输入顺序下第 $i$ 条边上写的标签。

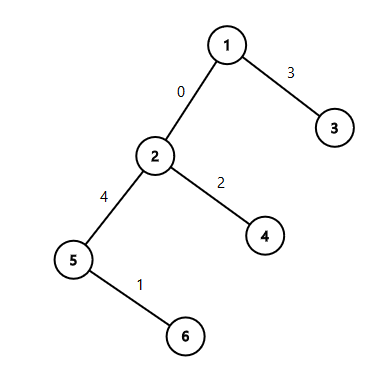
第二个样例中的树结构如下：  由 ChatGPT 4.1 翻译