CF1325C Ehab and Path-etic MEXs

You are given a tree consisting of $ n $ nodes. You want to write some labels on the tree's edges such that the following conditions hold: - Every label is an integer between $ 0 $ and $ n-2 $ inclusive. - All the written labels are distinct. - The largest value among $ MEX(u,v) $ over all pairs of nodes $ (u,v) $ is as small as possible. Here, $ MEX(u,v) $ denotes the smallest non-negative integer that isn't written on any edge on the unique simple path from node $ u $ to node $ v $ .

The first line contains the integer $ n $ ( $ 2 \le n \le 10^5 $ ) — the number of nodes in the tree. Each of the next $ n-1 $ lines contains two space-separated integers $ u $ and $ v $ ( $ 1 \le u,v \le n $ ) that mean there's an edge between nodes $ u $ and $ v $ . It's guaranteed that the given graph is a tree.

Output $ n-1 $ integers. The $ i^{th} $ of them will be the number written on the $ i^{th} $ edge (in the input order).

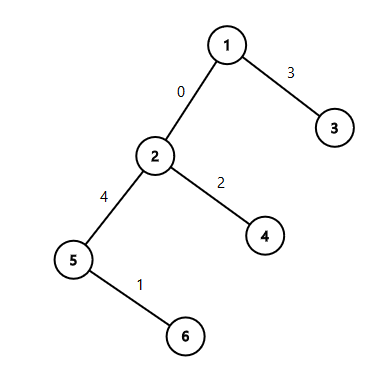
The tree from the second sample: