CF1325F Ehab's Last Theorem

现在是公元 5555 年。你有一张图，你想找到一个很长的环和一个很大的独立集，仅仅因为你可以。但现在，我们只需要找到其中之一。 给定一张连通图，包含 $n$ 个顶点，你可以选择以下两种方式之一： - 找到一个恰好包含 $ \lceil\sqrt{n}\rceil $ 个顶点的独立集。 - 找到一个长度至少为 $ \lceil\sqrt{n}\rceil $ 的简单环。 独立集是指任意两个顶点之间都没有边相连的顶点集合。简单环是指不包含重复顶点的环。我有一个证明可以说明你总能解决这两个问题中的一个，但它太长，放不下在这个边距里。

第一行包含两个整数 $n$ 和 $m$（$5 \le n \le 10^5$，$n-1 \le m \le 2 \cdot 10^5$），分别表示图的顶点数和边数。 接下来的 $m$ 行，每行包含两个用空格分隔的整数 $u$ 和 $v$（$1 \le u,v \le n$），表示在顶点 $u$ 和 $v$ 之间有一条边。保证图是连通的，且没有自环或重边。

如果你选择解决第一个问题，则第一行输出 "1"，接着一行输出 $ \lceil\sqrt{n}\rceil $ 个不超过 $n$ 的不同整数，表示所选独立集的顶点编号。 如果你选择解决第二个问题，则第一行输出 "2"，接着一行输出一个整数 $c$，表示找到的环的长度，下一行输出 $c$ 个不超过 $n$ 的不同整数，表示所选环中顶点的编号，按照环上出现的顺序输出。

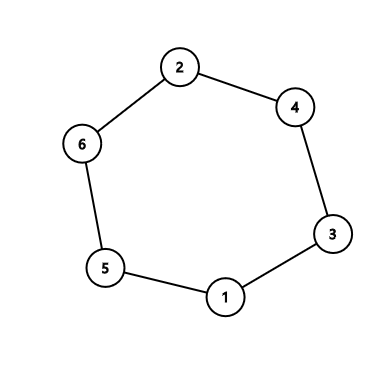
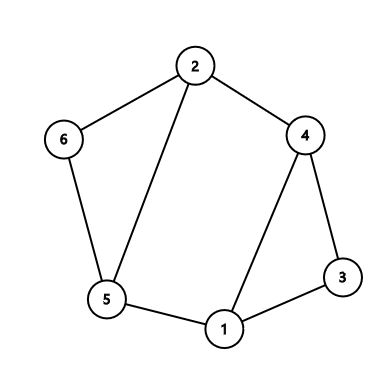
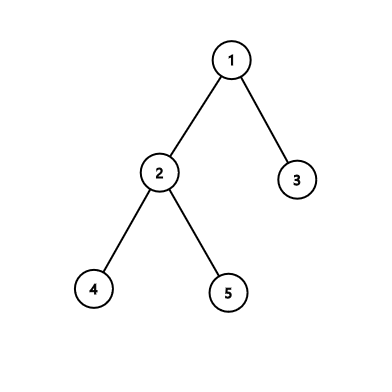
第一个样例中：  注意你可以任选其一，因此输出环 $2-4-3-1-5-6$ 也是可以的。 第二个样例中：  注意如果有多种答案，你可以输出任意一个，例如输出环 $2-5-6$ 也是可以的。 第三个样例中：  由 ChatGPT 4.1 翻译