CF1326G Spiderweb Trees

我们称一个有 $n$ 个顶点的图为平面树，每个顶点都有自己的点 $A_i = (x_i, y_i)$，且坐标为整数，若满足以下条件： - 所有点 $A_1, A_2, \ldots, A_n$ 都互不相同，且没有三个点共线。 - 该图是一棵树，即恰好有 $n-1$ 条边，且任意两点之间都存在一条路径。 - 对于所有的边对 $(s_1, f_1)$ 和 $(s_2, f_2)$，其中 $s_1 \neq s_2, s_1 \neq f_2, f_1 \neq s_2, f_1 \neq f_2$，线段 $A_{s_1}A_{f_1}$ 和 $A_{s_2}A_{f_2}$ 不相交。 设想一棵有 $n$ 个顶点的平面树。考虑点 $A_1, A_2, \ldots, A_n$ 的凸包。若对于所有 $1 \leq i \leq n$，下列条件均成立，则称这棵树为蜘蛛网树： - 树的所有叶子（度数 $\leq 1$ 的顶点）都在凸包的边界上。 - 凸包边界上的所有顶点都是叶子。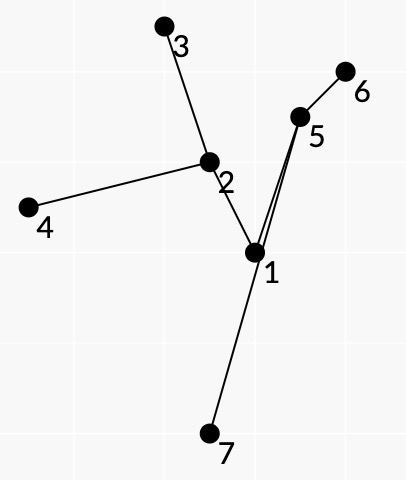 蜘蛛网树的一个例子如下：  点 $A_3, A_6, A_7, A_4$ 位于凸包上，树的叶子顶点为 $3, 6, 7, 4$。 更多例子请参考下方注释。 我们称顶点集合 $S \subset \{1, 2, \ldots, n\}$ 为树的子树，若对于 $S$ 中的任意一对顶点，存在一条仅包含 $S$ 中顶点的路径。注意，平面树的任意子树也是平面树。 给定一棵有 $n$ 个顶点的平面树。我们将集合 $\{1, 2, \ldots, n\}$ 的一个划分称为好的划分，若它被划分为若干非空子集 $A_1, A_2, \ldots, A_k$（即 $A_i \cap A_j = \emptyset$ 且 $A_1 \cup A_2 \cup \ldots \cup A_k = \{1, 2, \ldots, n\}$），并且对于所有 $1 \leq i \leq k$，子树 $A_i$ 都是蜘蛛网树。若存在某个集合只出现在一个划分中，则两个划分不同。 请计算好的划分的数量。由于答案可能很大，请输出对 $998\,244\,353$ 取模的结果。

第一行包含一个整数 $n$（$1 \leq n \leq 100$），表示树的顶点数。 接下来 $n$ 行，每行包含两个整数 $x_i, y_i$（$-10^9 \leq x_i, y_i \leq 10^9$），表示第 $i$ 个顶点 $A_i$ 的坐标。 接下来 $n-1$ 行，每行包含两个整数 $s, f$（$1 \leq s, f \leq n$），表示树中的一条边 $(s, f)$。 保证所有点都不同，且没有三点共线。并且保证给定的边和点的坐标描述的是一棵平面树。

输出一个整数，表示给定平面树的顶点的好的划分数量，对 $998\,244\,353$ 取模。

如果下列条件均成立，则称一个有 $n$ 个顶点的图为蜘蛛网树，每个顶点都有自己的点 $A_i = (x_i, y_i)$，且坐标为整数： - 所有点 $A_1, A_2, \ldots, A_n$ 都互不相同，且没有三点共线。 - 该图是一棵树，即恰好有 $n-1$ 条边，且任意两点之间都存在一条路径。 - 对于所有的边对 $(s_1, f_1)$ 和 $(s_2, f_2)$，其中 $s_1 \neq s_2, s_1 \neq f_2, f_1 \neq s_2, f_1 \neq f_2$，线段 $A_{s_1}A_{f_1}$ 和 $A_{s_2}A_{f_2}$ 不相交。 想象一棵有 $n$ 个顶点的蜘蛛网树。考虑点 $A_1, A_2, \ldots, A_n$ 的凸包。如果下列条件均成立，则称这棵树为蜘蛛网树： - 树的所有叶子（度数为 $1$ 的顶点）都在凸包的边界上。 - 凸包边界上的所有顶点都是叶子。 下图是蜘蛛网树的一个例子：  点 $A_3, A_6, A_7, A_4$ 位于凸包上，树的叶子顶点为 $3, 6, 7, 4$。 更多例子请参考下方注释。 我们称顶点集合 $S$ 为树的子树，若对于 $S$ 中的任意一对顶点，存在一条仅包含 $S$ 中顶点的路径，则该子树为树的子树。注意，平面树的任意子树也是平面树。 给定一棵有 $n$ 个顶点的蜘蛛网树。我们将集合的划分称为非空子集 $A_1, A_2, \ldots, A_k$ 的划分（如果在一个划分中存在某个集合，而在另一个划分中不存在，则两个划分不同）。 请计算所有好的划分的数量。由于答案可能很大，请输出对 $998\,244\,353$ 取模的结果。 由 ChatGPT 4.1 翻译