CF1328E Tree Queries

You are given a rooted tree consisting of $ n $ vertices numbered from $ 1 $ to $ n $ . The root of the tree is a vertex number $ 1 $ . A tree is a connected undirected graph with $ n-1 $ edges. You are given $ m $ queries. The $ i $ -th query consists of the set of $ k_i $ distinct vertices $ v_i[1], v_i[2], \dots, v_i[k_i] $ . Your task is to say if there is a path from the root to some vertex $ u $ such that each of the given $ k $ vertices is either belongs to this path or has the distance $ 1 $ to some vertex of this path.

The first line of the input contains two integers $ n $ and $ m $ ( $ 2 \le n \le 2 \cdot 10^5 $ , $ 1 \le m \le 2 \cdot 10^5 $ ) — the number of vertices in the tree and the number of queries. Each of the next $ n-1 $ lines describes an edge of the tree. Edge $ i $ is denoted by two integers $ u_i $ and $ v_i $ , the labels of vertices it connects $ (1 \le u_i, v_i \le n, u_i \ne v_i $ ). It is guaranteed that the given edges form a tree. The next $ m $ lines describe queries. The $ i $ -th line describes the $ i $ -th query and starts with the integer $ k_i $ ( $ 1 \le k_i \le n $ ) — the number of vertices in the current query. Then $ k_i $ integers follow: $ v_i[1], v_i[2], \dots, v_i[k_i] $ ( $ 1 \le v_i[j] \le n $ ), where $ v_i[j] $ is the $ j $ -th vertex of the $ i $ -th query. It is guaranteed that all vertices in a single query are distinct. It is guaranteed that the sum of $ k_i $ does not exceed $ 2 \cdot 10^5 $ ( $ \sum\limits_{i=1}^{m} k_i \le 2 \cdot 10^5 $ ).

For each query, print the answer — "YES", if there is a path from the root to some vertex $ u $ such that each of the given $ k $ vertices is either belongs to this path or has the distance $ 1 $ to some vertex of this path and "NO" otherwise.

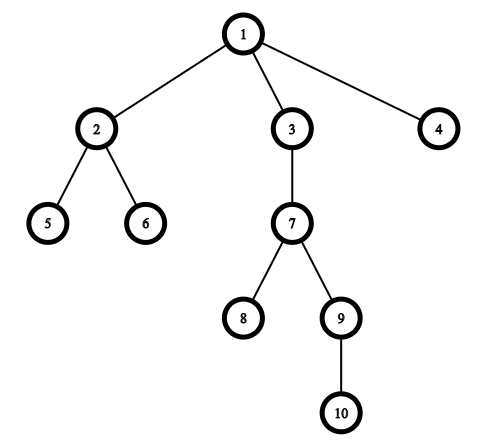
The picture corresponding to the example:  Consider the queries. The first query is $ [3, 8, 9, 10] $ . The answer is "YES" as you can choose the path from the root $ 1 $ to the vertex $ u=10 $ . Then vertices $ [3, 9, 10] $ belong to the path from $ 1 $ to $ 10 $ and the vertex $ 8 $ has distance $ 1 $ to the vertex $ 7 $ which also belongs to this path. The second query is $ [2, 4, 6] $ . The answer is "YES" as you can choose the path to the vertex $ u=2 $ . Then the vertex $ 4 $ has distance $ 1 $ to the vertex $ 1 $ which belongs to this path and the vertex $ 6 $ has distance $ 1 $ to the vertex $ 2 $ which belongs to this path. The third query is $ [2, 1, 5] $ . The answer is "YES" as you can choose the path to the vertex $ u=5 $ and all vertices of the query belong to this path. The fourth query is $ [4, 8, 2] $ . The answer is "YES" as you can choose the path to the vertex $ u=9 $ so vertices $ 2 $ and $ 4 $ both have distance $ 1 $ to the vertex $ 1 $ which belongs to this path and the vertex $ 8 $ has distance $ 1 $ to the vertex $ 7 $ which belongs to this path. The fifth and the sixth queries both have answer "NO" because you cannot choose suitable vertex $ u $ .