CF1328E Tree Queries

给定一棵有 $n$ 个顶点的有根树，顶点编号为 $1$ 到 $n$，树的根为顶点 $1$。 树是一个连通无向图，包含 $n-1$ 条边。 你需要回答 $m$ 个询问。第 $i$ 个询问给出一个包含 $k_i$ 个不同顶点的集合 $v_i[1], v_i[2], \dots, v_i[k_i]$。你的任务是判断是否存在一条从根到某个顶点 $u$ 的路径，使得给定的 $k$ 个顶点中的每一个，要么在这条路径上，要么与这条路径上的某个顶点的距离为 $1$。

输入的第一行包含两个整数 $n$ 和 $m$（$2 \le n \le 2 \cdot 10^5$，$1 \le m \le 2 \cdot 10^5$），分别表示树的顶点数和询问数。 接下来的 $n-1$ 行，每行描述树的一条边。第 $i$ 条边由两个整数 $u_i$ 和 $v_i$ 表示，表示这条边连接顶点 $u_i$ 和 $v_i$（$1 \le u_i, v_i \le n, u_i \ne v_i$）。 保证给定的边构成一棵树。 接下来的 $m$ 行，每行描述一个询问。第 $i$ 行以整数 $k_i$ 开头（$1 \le k_i \le n$），表示当前询问包含的顶点数。接下来有 $k_i$ 个整数：$v_i[1], v_i[2], \dots, v_i[k_i]$（$1 \le v_i[j] \le n$），表示第 $i$ 个询问的顶点。 保证每个询问中的顶点互不相同。 保证所有 $k_i$ 的总和不超过 $2 \cdot 10^5$（$\sum\limits_{i=1}^{m} k_i \le 2 \cdot 10^5$）。

对于每个询问，输出一行答案。如果存在一条从根到某个顶点 $u$ 的路径，使得每个给定的 $k$ 个顶点都在这条路径上，或与路径上的某个顶点的距离为 $1$，则输出 "YES"；否则输出 "NO"。

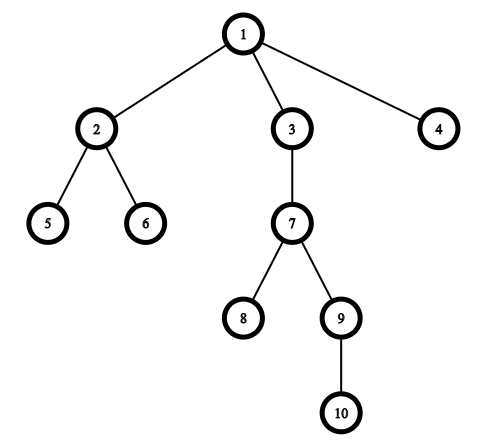
与样例对应的树结构如下图所示：  考虑以下几个询问： 第一个询问为 $[3, 8, 9, 10]$。答案为 "YES"，因为可以选择从根 $1$ 到顶点 $u=10$ 的路径。此时顶点 $[3, 9, 10]$ 都在路径上，顶点 $8$ 与路径上的顶点 $7$ 距离为 $1$。 第二个询问为 $[2, 4, 6]$。答案为 "YES"，因为可以选择到顶点 $u=2$ 的路径。此时顶点 $4$ 与路径上的顶点 $1$ 距离为 $1$，顶点 $6$ 与路径上的顶点 $2$ 距离为 $1$。 第三个询问为 $[2, 1, 5]$。答案为 "YES"，可以选择到顶点 $u=5$ 的路径，所有询问中的顶点都在路径上。 第四个询问为 $[4, 8, 2]$。答案为 "YES"，可以选择到顶点 $u=9$ 的路径，此时顶点 $2$ 和 $4$ 都与路径上的顶点 $1$ 距离为 $1$，顶点 $8$ 与路径上的顶点 $7$ 距离为 $1$。 第五和第六个询问的答案均为 "NO"，因为无法选择合适的顶点 $u$。 由 ChatGPT 4.1 翻译