CF1332F Independent Set
题目描述
Eric 是一名图论课的老师。这天,Eric 上的是关于点独立集和边导出子图的内容。
给出一张图 $G = (V, E)$,一个点独立集是指点的一个子集 $V' \subset V$,满足对于任意一对 $u, v \in V'$,$(u, v) \not \in E$(也就是说,不存在一条 $E$ 中的边,连接的两端点同在 $V'$ 中)。
一个边导出子图包含了边的一个子集 $E' \subset E$,和原图上所有与 $E'$ 中至少一条边有相邻的点。
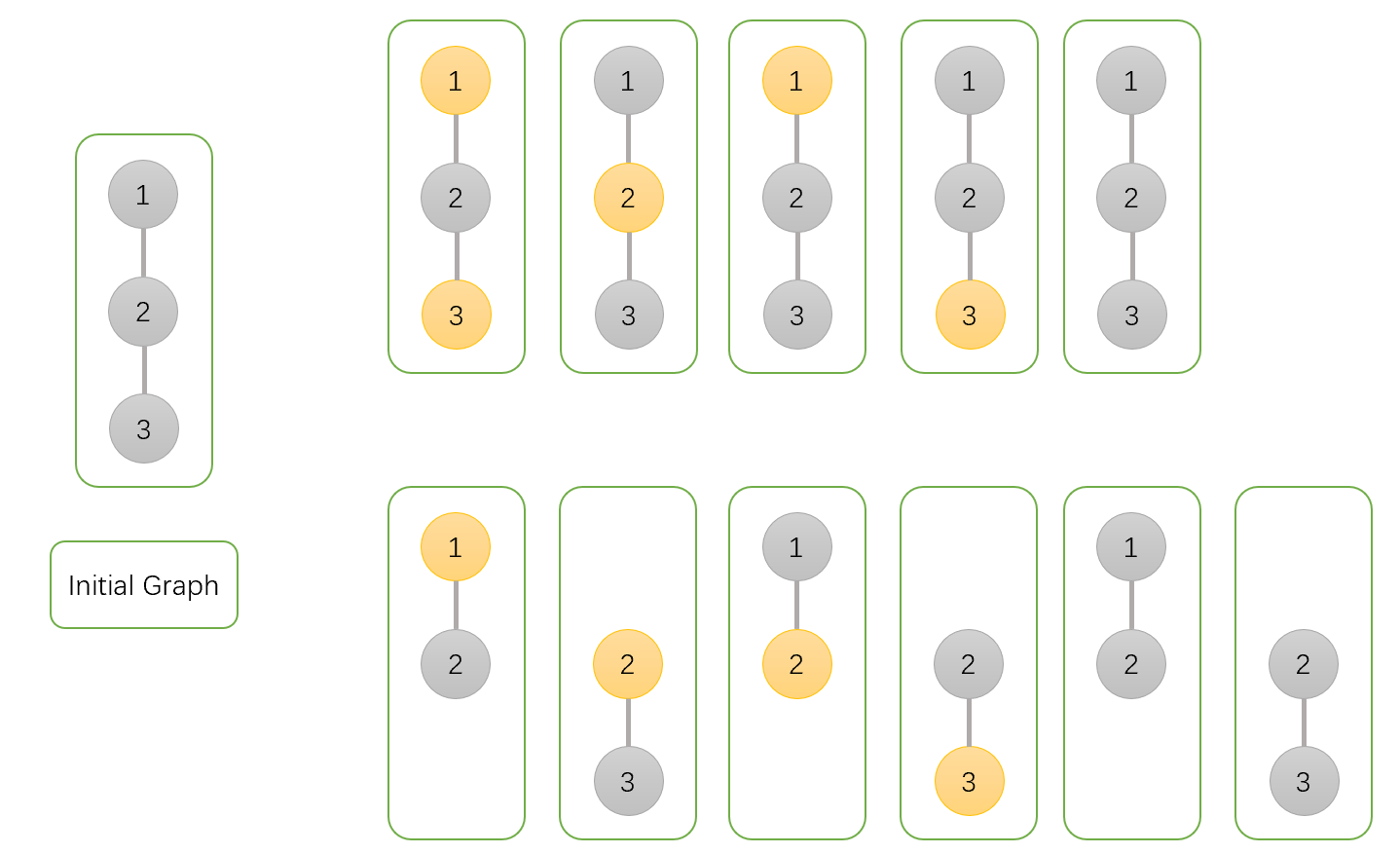
设有 $E' \subset E$,定义 $G[E']$ 表示一个以 $E'$ 作为边集的边导出子图。这是对于上述定义的一个图例说明:
为了帮助他的学生们熟悉这些定义,Eric 留下了这样一个问题作为练习:
给出一棵树 $G = (V, E)$,对于 $G$ 中所有的非空边导出子图 $H$,计算 $w(H)$ 之和。其中 $w(H)$ 表示 $H$ 中点独立集的种类数。形式化地说,求 $\sum \limits_{\emptyset \not= E' \subset E} w(G[E'])$。
为了向 Eric 展现你比他的学生们都要厉害,请你尽可能快地求出正确答案。注意答案可能很大,你需要输出它对 $998, 244, 353$ 取模的值。
输入格式
第一行输入一个整数 $n ~ (2 \le n \le 3 \cdot 10 ^ 5)$,表示 $G$ 中的点数。
接下来 $n - 1$ 行,每行输入两个整数 $u, v ~ (1 \le u, v \le n; u \neq v)$,表示给定树中的边。
保证输入的边形成一棵树。
输出格式
输出一行一个整数,表示所求答案对 $998, 244, 353$ 取模的值。
说明/提示
For the second example, all independent sets are listed below.