CF1334E Divisor Paths

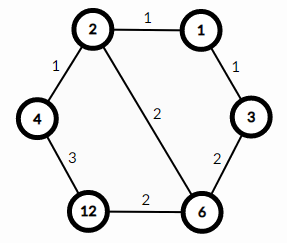
给定一个正整数 $D$，我们基于它构建如下图： - 每个顶点是 $D$ 的一个约数（不要求是质数，$1$ 和 $D$ 本身也包括在内）； - 对于两个顶点 $x$ 和 $y$（$x > y$），如果 $x$ 能被 $y$ 整除且 $\frac{x}{y}$ 是质数，则在它们之间连一条无向边； - 边的权值为 $x$ 的约数中不是 $y$ 的约数的个数。 例如，$D=12$ 时的图如下：  边 $(4,12)$ 的权值为 $3$，因为 $12$ 的约数为 $[1,2,3,4,6,12]$，$4$ 的约数为 $[1,2,4]$，因此 $12$ 有 $3$ 个约数不是 $4$ 的约数——$[3,6,12]$。 $3$ 和 $2$ 之间没有边，因为 $3$ 不能被 $2$ 整除。$12$ 和 $3$ 之间没有边，因为 $\frac{12}{3}=4$ 不是质数。 在该图中，某两个顶点 $v$ 和 $u$ 之间一条路径的长度为路径上所有边的权值之和。例如，路径 $[(1,2),(2,6),(6,12),(12,4),(4,2),(2,6)]$ 的长度为 $1+2+2+3+1+2=11$。空路径的长度为 $0$。 因此，两个顶点 $v$ 和 $u$ 之间的最短路径，就是所有可能路径中长度最小的那一条。 如果两条路径 $a$ 和 $b$ 的边数不同，或者存在某个位置 $i$ 使得 $a_i$ 和 $b_i$ 是不同的边，则认为这两条路径不同。 现在给定 $q$ 个询问，每个询问如下： - $v\ u$ —— 计算从顶点 $v$ 到顶点 $u$ 的最短路径的数量。 每个询问的答案可能很大，请对 $998244353$ 取模后输出。

第一行包含一个整数 $D$（$1 \le D \le 10^{15}$）——用于构建图的数。 第二行包含一个整数 $q$（$1 \le q \le 3 \times 10^5$）——询问的数量。 接下来 $q$ 行，每行包含两个整数 $v$ 和 $u$（$1 \le v, u \le D$）。保证 $D$ 能被 $v$ 和 $u$ 整除（即 $v$ 和 $u$ 都是 $D$ 的约数）。

输出 $q$ 个整数，每个询问输出一行，表示从给定的两个顶点之间的最短路径数量，对 $998244353$ 取模。

在第一个样例中： - 第一个询问只有空路径，长度为 $0$； - 第二个询问有路径 $[(12,4),(4,2),(2,1)]$（长度 $3+1+1=5$）、$[(12,6),(6,2),(2,1)]$（长度 $2+2+1=5$）和 $[(12,6),(6,3),(3,1)]$（长度 $2+2+1=5$）； - 第三个询问只有路径 $[(3,1),(1,2),(2,4)]$（长度 $1+1+1=3$）。 由 ChatGPT 4.1 翻译