CF1338D Nested Rubber Bands

你有一棵包含 $n$ 个顶点的树。你需要将这棵树转换为无限大平面上的 $n$ 个橡皮筋。转换规则如下： - 对于每一对顶点 $a$ 和 $b$，当且仅当树中存在一条连接 $a$ 和 $b$ 的边时，橡皮筋 $a$ 和橡皮筋 $b$ 必须相交。 - 每根橡皮筋的形状必须是一个简单环。换句话说，橡皮筋是一个不自交的环。 现在定义如下概念： - 如果橡皮筋 $a$ 包含橡皮筋 $b$，当且仅当橡皮筋 $b$ 在橡皮筋 $a$ 的区域内部，且它们不相交。 - 一组橡皮筋 $a_{1}, a_{2}, \ldots, a_{k}$（$k \ge 2$）是嵌套的，当且仅当对于所有 $i$（$2 \le i \le k$），都有 $a_{i-1}$ 包含 $a_{i}$。 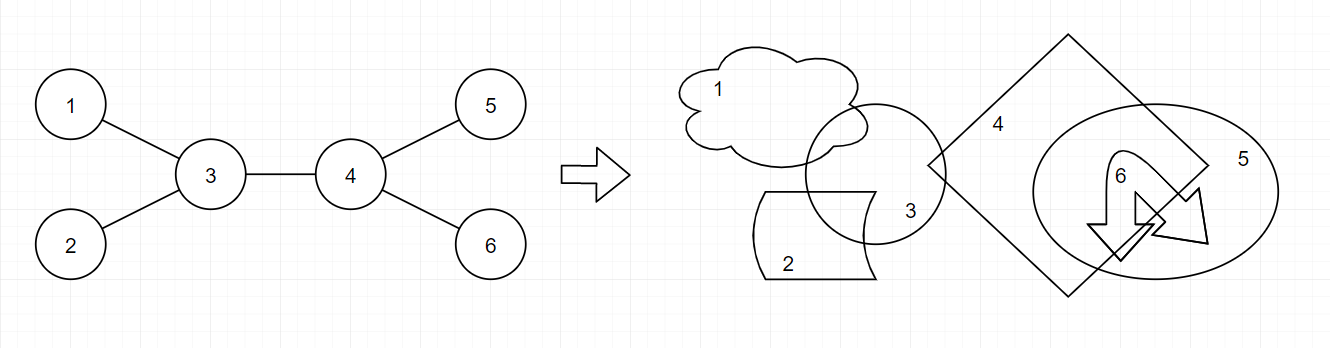 这是一次转换的示例。注意橡皮筋 $5$ 和 $6$ 是嵌套的。可以证明，在给定的约束下，总是可以进行一次转换，并得到一组嵌套的橡皮筋序列。 对于给定的树，能得到的嵌套橡皮筋序列的最大长度是多少？请输出答案。

第一行包含一个整数 $n$（$3 \le n \le 10^{5}$），表示树的顶点数。 接下来的 $n-1$ 行中，第 $i$ 行包含两个整数 $a_{i}$ 和 $b_{i}$（$1 \le a_{i} < b_{i} \le n$），表示在 $a_{i}$ 和 $b_{i}$ 之间有一条边。保证给定的图是一棵 $n$ 个顶点的树。

输出答案。

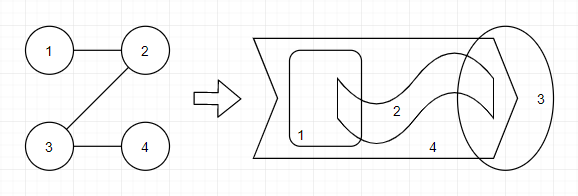
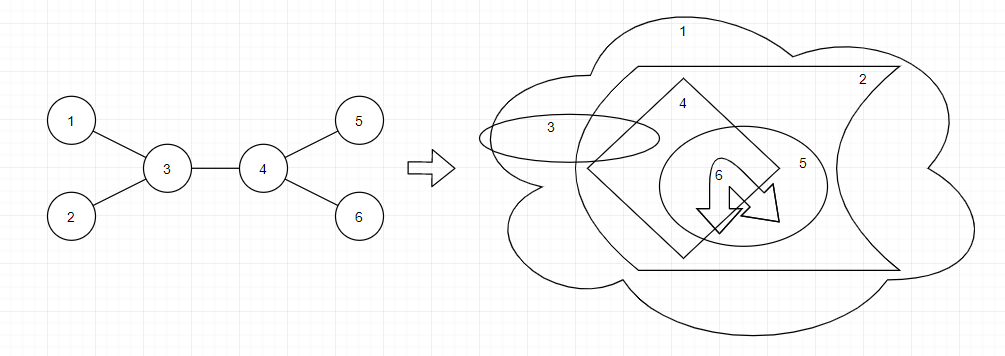在第一个样例中，你可以通过如下转换得到一组长度为 $4$ 的嵌套橡皮筋序列（$1$、$2$、$5$ 和 $6$）。当然，也存在其他方式可以得到长度为 $4$ 的嵌套橡皮筋序列。然而，无法用给定的树得到长度为 $5$ 或更长的嵌套橡皮筋序列。 你可以在下图中看到第二个样例的一种可能的转换方式。  由 ChatGPT 4.1 翻译