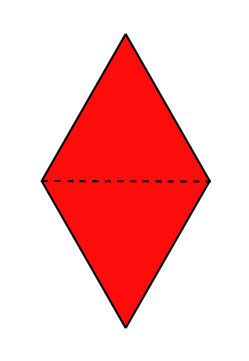
CF1339A Filling Diamonds

You have integer $ n $ . Calculate how many ways are there to fully cover belt-like area of $ 4n-2 $ triangles with diamond shapes. Diamond shape consists of two triangles. You can move, rotate or flip the shape, but you cannot scale it. $ 2 $ coverings are different if some $ 2 $ triangles are covered by the same diamond shape in one of them and by different diamond shapes in the other one. Please look at pictures below for better understanding. 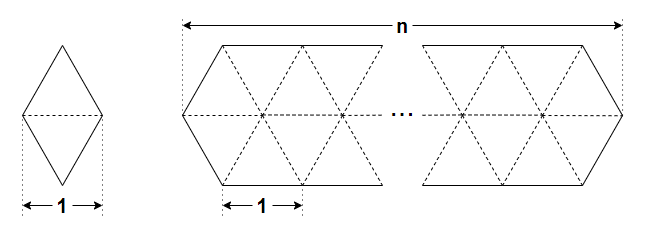 On the left you can see the diamond shape you will use, and on the right you can see the area you want to fill.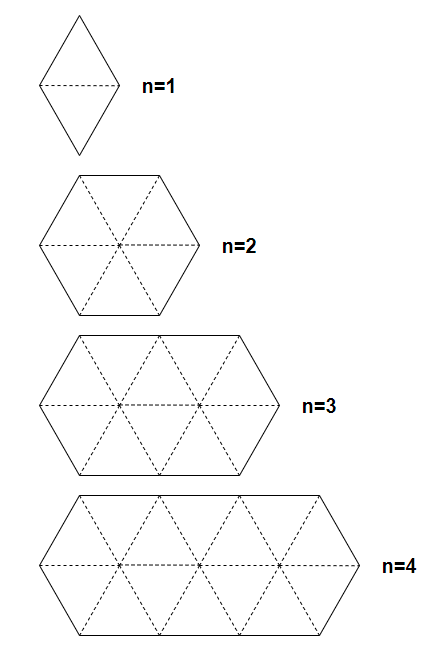 These are the figures of the area you want to fill for $ n = 1, 2, 3, 4 $ . You have to answer $ t $ independent test cases.

The first line contains a single integer $ t $ ( $ 1 \le t \le 10^{4} $ ) — the number of test cases. Each of the next $ t $ lines contains a single integer $ n $ ( $ 1 \le n \le 10^{9} $ ).

For each test case, print the number of ways to fully cover belt-like area of $ 4n-2 $ triangles using diamond shape. It can be shown that under given constraints this number of ways doesn't exceed $ 10^{18} $ .

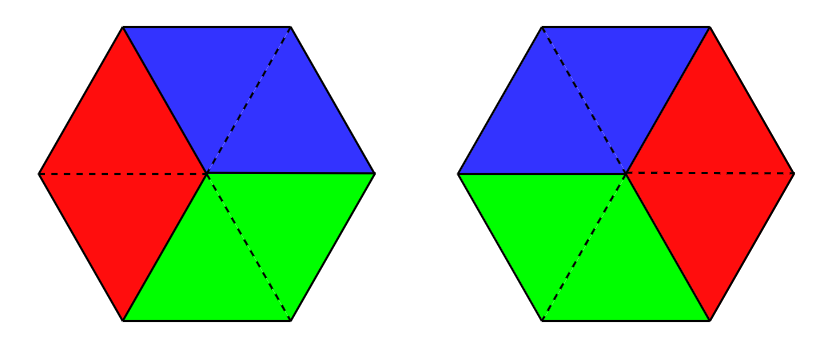In the first test case, there are the following $ 2 $ ways to fill the area: In the second test case, there is a unique way to fill the area: