CF1343E Weights Distributing

给定一个无向无权图，包含 $n$ 个顶点和 $m$ 条边（代表 Bertown 的地图），以及一个长度为 $m$ 的价格数组 $p$。保证任意两点之间都存在路径。 Mike 计划从顶点（区域）$a$ 出发到顶点（区域）$b$，然后从顶点（区域）$b$ 到顶点（区域）$c$。他可以多次经过同一个区域。但是有一个问题：城市当局想要为每条道路设置一个价格，每当有人经过一条道路时，都需要支付该道路对应的价格（每经过一次都要付费）。价格列表 $p$ 已经准备好，他们只需要将其分配给城镇中的所有道路，使得每个价格恰好对应一条道路。 你是 Mike 的好朋友（同时也是 Bertown 的市长），你想帮助他让这次旅行的花费尽可能少。因此，你的任务是分配道路的价格，使得 Mike 选择最优路径时，这次旅行的总花费最小。注意，旅行开始后不能再重新分配价格。 你需要回答 $t$ 个独立的测试用例。

输入的第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。接下来是 $t$ 个测试用例。 每个测试用例的第一行包含五个整数 $n, m, a, b, c$（$2 \le n \le 2 \times 10^5$，$n-1 \le m \le \min(\frac{n(n-1)}{2}, 2 \times 10^5)$，$1 \le a, b, c \le n$），分别表示顶点数、边数，以及 Mike 旅行经过的区域编号。 测试用例的第二行包含 $m$ 个整数 $p_1, p_2, \dots, p_m$（$1 \le p_i \le 10^9$），表示价格数组中的每个价格。 接下来的 $m$ 行，每行包含两个整数 $v_i, u_i$（$1 \le v_i, u_i \le n$，$u_i \ne v_i$），表示一条连接 $v_i$ 和 $u_i$ 的边。图中没有自环和重边，即对于每对 $(v_i, u_i)$，不存在其他的 $(v_i, u_i)$ 或 $(u_i, v_i)$，并且 $v_i \ne u_i$。保证给定的图是连通的。 保证所有测试用例中 $n$ 的总和不超过 $2 \times 10^5$，$m$ 的总和也不超过 $2 \times 10^5$（$\sum n \le 2 \times 10^5$，$\sum m \le 2 \times 10^5$）。

对于每个测试用例，输出一个整数，表示在最优分配价格的情况下，Mike 这次旅行的最小可能花费。

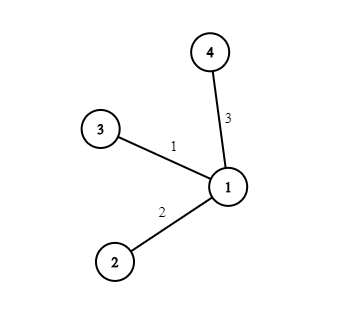
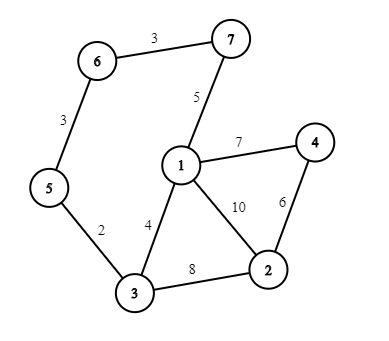
以下是样例第一个测试用例的一种可能的解决方案：  以下是样例第二个测试用例的一种可能的解决方案：  由 ChatGPT 4.1 翻译