CF1344E Train Tracks

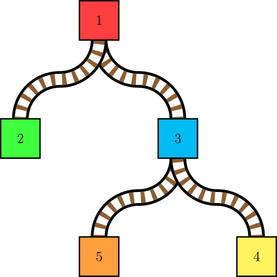
没错。我是 Purdue 的学生，我毫不羞耻地出了一道关于火车的题目。 现在有 $n$ 个车站和 $m$ 列火车。车站之间通过 $n-1$ 条单向铁路线连接，形成一棵以车站 $1$ 为根的树。所有铁路线的方向都是从根车站 $1$ 指向叶子节点。每条铁路线连接车站 $u$ 到车站 $v$，距离为 $d$，表示从 $u$ 到 $v$ 需要 $d$ 单位时间。每个有至少一条出边的车站都配有一个“道岔”，它决定进入该站的火车将被引导到哪个子车站。例如，可能如下图所示：  在上图中，车站 $1$ 和 $3$ 的道岔分别指向车站 $2$ 和 $4$。初始时，所有车站都没有火车。第 $i$ 列火车将在时间 $t_i$ 进入车站 $1$。从时间 $1$ 开始，每个单位时间内，依次进行以下两个步骤： 1. 你可以将至多一个车站的道岔切换到指向另一个子车站。道岔的切换在第 2 步之前生效。 2. 对于每一列停在车站 $u$ 的火车，它会被引导到 $u$ 的道岔所指向的车站 $v$。如果 $u$ 到 $v$ 的铁路线距离为 $d$，那么这列火车将在 $d$ 单位时间后到达车站 $v$。 每列火车都有一个目标车站 $s_i$。当它到达 $s_i$ 时，将永久停留在那里。如果某一时刻火车被引导到了错误的方向，导致无论如何切换道岔都无法到达 $s_i$，那么它会立即爆炸。 请你在最优切换道岔的情况下，求出第一次爆炸最晚可能发生的时间（如果可以避免所有爆炸则输出 $-1$），以及为此所需的最少道岔切换次数。

第一行包含两个整数 $n$ 和 $m$（$1\le n,m\le 10^5$），分别表示车站数和火车数。 接下来 $n-1$ 行描述铁路线。第 $i$ 行包含三个整数 $u,v,d$（$1\le u,v\le n$，$1\le d\le 10^9$），表示一条从车站 $u$ 到车站 $v$ 的距离为 $d$ 的铁路线。保证所有铁路线构成一棵以车站 $1$ 为根的树。每个车站 $u$ 的道岔初始指向输入中最后出现的从 $u$ 出发的铁路线。 接下来 $m$ 行描述火车。第 $i$ 行包含两个整数 $s_i,t_i$（$1\le s_i\le n$，$1\le t_1

输出两个整数：第一次爆炸最晚可能发生的时间（如果可以避免所有爆炸则输出 $-1$），以及为此所需的最少道岔切换次数。

对于第一个样例，时间线如下： - 时间 $1$，火车 $1$ 进入车站 $1$。我们将车站 $1$ 的道岔切换指向车站 $2$。火车 $1$ 被引导至车站 $2$。 - 时间 $2$，火车 $2$ 进入车站 $1$，火车 $1$ 到达车站 $2$ 并永久停留。我们将车站 $1$ 的道岔切换指向车站 $3$。火车 $2$ 被引导至车站 $3$。 - 时间 $4$，火车 $2$ 到达车站 $3$。我们将车站 $3$ 的道岔切换指向车站 $4$。火车 $2$ 被引导至车站 $4$。 - 时间 $5$，火车 $2$ 到达车站 $4$ 并永久停留。 - 时间 $6$，火车 $3$ 进入车站 $1$。我们将车站 $1$ 的道岔切换指向车站 $2$。火车 $3$ 被引导至车站 $2$。 - 时间 $7$，火车 $3$ 到达车站 $2$ 并永久停留。我们将车站 $3$ 的道岔切换指向车站 $5$。 - 时间 $10$，火车 $4$ 进入车站 $1$。我们将车站 $1$ 的道岔切换指向车站 $3$。火车 $4$ 被引导至车站 $3$。 - 时间 $12$，火车 $4$ 到达车站 $3$。火车 $4$ 被引导至车站 $5$。 - 时间 $15$，火车 $4$ 到达车站 $5$ 并永久停留。 对于第二个样例，不进行任何切换。在时间 $4$，火车 $2$ 被引导至车站 $5$，火车 $4$ 被引导至车站 $3$，它们都爆炸了。无法在时间 $4$ 之后避免爆炸。 对于第三个样例，记一次道岔切换为 $(u\to v,t)$，表示在时间 $t$ 将车站 $u$ 的道岔指向车站 $v$。一种方案是进行如下 $4$ 次切换：$(1\to 2,1)$，$(1\to 3,2)$，$(7\to 8,5)$，$(5\to 6,8)$。在时间 $11$，火车 $4$、$5$、$6$ 爆炸。无法在时间 $11$ 之后避免爆炸。 由 ChatGPT 4.1 翻译