CF1349C Orac and Game of Life

请注意本题不同寻常的内存限制。 Orac 喜欢玩游戏。最近他想出了一个新游戏，叫做“生命游戏”。 你需要在一个黑白网格上玩这个游戏，网格有 $n$ 行 $m$ 列。每个格子要么是黑色，要么是白色。 每一轮游戏（初始为第 $0$ 轮），每个格子的颜色会根据以下规则变化： - 如果当前轮次该格子没有相邻格子颜色和它相同，则下一轮它的颜色保持不变。 - 否则，下一轮它的颜色会变为不同的颜色。 如果两个格子有公共边，则它们是相邻的。 现在 Orac 给定了一个初始状态，他想知道对于第 $i$ 行第 $j$ 列的格子，在第 $p$ 轮时它的颜色是什么。他可能会多次询问你这些问题。

第一行包含三个整数 $n,m,t\ (1\le n,m\le 1000, 1\le t\le 100\,000)$，分别表示行数、列数和 Orac 的询问次数。 接下来的 $n$ 行，每行包含一个长度为 $m$ 的二进制字符串，第 $i$ 行第 $j$ 个字符表示格子 $(i,j)$ 的初始颜色。'0' 表示白色，'1' 表示黑色。 接下来的 $t$ 行，每行包含三个整数 $i,j,p\ (1\le i\le n, 1\le j\le m, 1\le p\le 10^{18})$，表示 Orac 的一次询问。

输出 $t$ 行，第 $i$ 行输出 Orac 第 $i$ 个询问的答案。如果该格子为黑色，输出 '1'；否则输出 '0'。

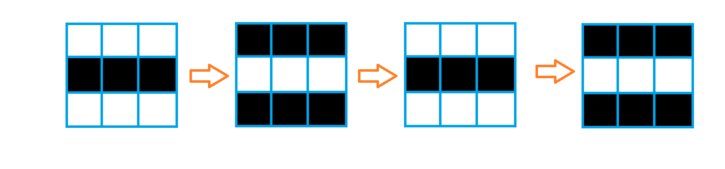
 对于第一个样例，上图展示了初始状态以及第 $1$、$2$、$3$ 轮时各格子的颜色。可以看到，第 $1$ 行第 $1$ 列在第 $1$ 轮时是黑色，第 $2$ 行第 $2$ 列在第 $2$ 轮时是黑色，第 $3$ 行第 $3$ 列在第 $3$ 轮时也是黑色。 对于第二个样例，你可以证明所有格子的颜色都不会发生变化。 由 ChatGPT 4.1 翻译