CF1349C Orac and Game of Life
题目描述
请注意本题不同寻常的内存限制。
Orac 喜欢玩游戏。最近他想出了一个新游戏,叫做“生命游戏”。
你需要在一个黑白网格上玩这个游戏,网格有 $n$ 行 $m$ 列。每个格子要么是黑色,要么是白色。
每一轮游戏(初始为第 $0$ 轮),每个格子的颜色会根据以下规则变化:
- 如果当前轮次该格子没有相邻格子颜色和它相同,则下一轮它的颜色保持不变。
- 否则,下一轮它的颜色会变为不同的颜色。
如果两个格子有公共边,则它们是相邻的。
现在 Orac 给定了一个初始状态,他想知道对于第 $i$ 行第 $j$ 列的格子,在第 $p$ 轮时它的颜色是什么。他可能会多次询问你这些问题。
输入格式
第一行包含三个整数 $n,m,t\ (1\le n,m\le 1000, 1\le t\le 100\,000)$,分别表示行数、列数和 Orac 的询问次数。
接下来的 $n$ 行,每行包含一个长度为 $m$ 的二进制字符串,第 $i$ 行第 $j$ 个字符表示格子 $(i,j)$ 的初始颜色。'0' 表示白色,'1' 表示黑色。
接下来的 $t$ 行,每行包含三个整数 $i,j,p\ (1\le i\le n, 1\le j\le m, 1\le p\le 10^{18})$,表示 Orac 的一次询问。
输出格式
输出 $t$ 行,第 $i$ 行输出 Orac 第 $i$ 个询问的答案。如果该格子为黑色,输出 '1';否则输出 '0'。
说明/提示
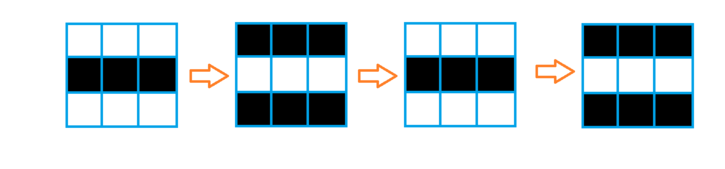
对于第一个样例,上图展示了初始状态以及第 $1$、$2$、$3$ 轮时各格子的颜色。可以看到,第 $1$ 行第 $1$ 列在第 $1$ 轮时是黑色,第 $2$ 行第 $2$ 列在第 $2$ 轮时是黑色,第 $3$ 行第 $3$ 列在第 $3$ 轮时也是黑色。
对于第二个样例,你可以证明所有格子的颜色都不会发生变化。
由 ChatGPT 4.1 翻译