CF1359F RC Kaboom Show

你知道，现在要在同一个地方举办一场有许多参与者和观众的表演是很困难的。不过，你并没有放弃举办汽车碰撞表演的梦想！你决定用遥控汽车代替真车，把活动命名为“Remote Control Kaboom Show”，并将整个过程在线直播。 为此，你准备了一个竞技场——一个无限的二维平面。你还买了 $n$ 辆遥控汽车，并把它们放在竞技场上。不幸的是，你买的这些车只能直行，不能左转、右转或掉头。因此，你还需要把每辆车朝你希望它前进的方向摆好。 具体来说，对于每辆第 $i$ 辆车（$1 \le i \le n$），你选择了它的初始位置 $(x_i, y_i)$ 和一个方向向量 $(dx_i, dy_i)$。此外，每辆车都有一个恒定的速度 $s_i$ 单位/秒。因此，当第 $i$ 辆车被启动后，它会以恒定速度 $s_i$，沿着 $(dx_i, dy_i)$ 方向，从 $(x_i, y_i)$ 开始移动。 表演的目标是让两辆车尽快相撞！你注意到，如果在表演开始时同时启动所有汽车，往往不会发生任何碰撞。因此，你计划在某个时刻 $t_i$ 启动第 $i$ 辆车。你还没有决定所有 $t_i$ 的具体数值。注意，$t_i$ 不必为整数，且对于任意 $i, j$，$t_i$ 允许等于 $t_j$。 表演从时间 $0$ 开始。当有两辆不同的车 $i$ 和 $j$（$i \ne j$）在同一时刻到达同一坐标时，表演结束。表演的持续时间为开始到结束的时间间隔。 你可以自由选择所有 $t_i$，请问能否安排一次碰撞？如果可以，请输出最短的表演持续时间；否则，输出 "No show :("。 如果你的答案的绝对误差或相对误差不超过 $10^{-6}$，则视为正确。 形式化地，设你的答案为 $a$，标准答案为 $b$，当且仅当 $ \frac{|a - b|}{\max{(1, |b|)}} \le 10^{-6} $ 时，答案被接受。

第一行包含一个整数 $n$（$1 \le n \le 25000$），表示汽车的数量。 接下来的 $n$ 行，每行包含五个整数 $x_i, y_i, dx_i, dy_i, s_i$（$-10^3 \le x_i, y_i \le 10^3$；$1 \le |dx_i| \le 10^3$；$1 \le |dy_i| \le 10^3$；$1 \le s_i \le 10^3$），分别表示第 $i$ 辆车的初始位置、方向向量和速度。 保证所有汽车的初始位置各不相同（即对于 $i \ne j$，$(x_i, y_i) \ne (x_j, y_j)$）。

如果可以通过选择所有 $t_i$ 安排一次碰撞，请输出最短的表演持续时间。否则，输出 "No show :("。 你的答案被认为是正确的，当且仅当其绝对误差或相对误差不超过 $10^{-6}$。

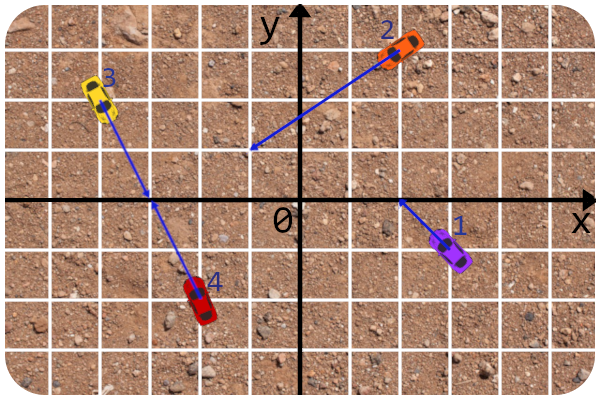
下面是第一个样例的示意图：  最快相撞的是第 $2$ 辆车和第 $4$ 辆车。可以在 $0$ 时刻启动第 $2$ 辆车，在约 $0.096762$ 时刻启动第 $4$ 辆车，其余两辆车在任意时刻启动。这样，第 $2$ 辆车和第 $4$ 辆车将在约 $0.585902$ 时刻相撞。下图为碰撞瞬间的示意：  下面是第二个样例的示意图：  由 ChatGPT 4.1 翻译