CF1363E Tree Shuffling

Ashish 有一棵包含 $n$ 个节点的树，节点编号为 $1$ 到 $n$，以节点 $1$ 为根。树中第 $i$ 个节点有一个代价 $a_i$，并且写有一个二进制数字 $b_i$。他希望最终每个节点 $i$ 上写有目标二进制数字 $c_i$。 为此，他可以进行如下操作任意次： - 从任意节点 $u$ 的子树中选择任意 $k$ 个节点，并随意打乱这 $k$ 个节点上的数字，操作的代价为 $k \cdot a_u$。其中 $k$ 可以从 $1$ 到 $u$ 的子树大小任意选择。 他希望通过若干次操作，使得每个节点最终都拥有其目标数字。 请你帮助他计算使所有节点达到目标数字所需的最小总代价，或者判断是否无法实现。

第一行包含一个整数 $n$ $(1 \leq n \leq 2 \times 10^5)$，表示树的节点数。 接下来 $n$ 行，每行包含三个用空格分隔的整数 $a_i$、$b_i$、$c_i$ $(1 \leq a_i \leq 10^9, 0 \leq b_i, c_i \leq 1)$，分别表示第 $i$ 个节点的代价、初始数字和目标数字。 接下来 $n-1$ 行，每行包含两个整数 $u$、$v$ $(1 \leq u, v \leq n, u \ne v)$，表示树中存在一条连接节点 $u$ 和 $v$ 的边。

输出使所有节点达到目标数字所需的最小总代价。如果无法实现，输出 $-1$。

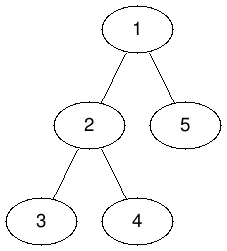
样例 $1$ 和 $2$ 所对应的树如下：  在样例 $1$ 中，我们可以选择节点 $1$，$k=4$，总代价为 $4 \cdot 1 = 4$，选择节点 $\{1,2,3,5\}$，打乱它们的数字后即可得到所有节点的目标数字。 在样例 $2$ 中，我们可以选择节点 $1$，$k=2$，总代价为 $10000 \cdot 2$，选择节点 $\{1,5\}$，交换它们的数字；同理，选择节点 $2$，$k=2$，总代价为 $2000 \cdot 2$，选择节点 $\{2,3\}$，交换它们的数字，最终所有节点都能达到目标数字。 在样例 $3$ 中，无法得到目标数字，因为初始状态下没有任何节点上写有数字 $1$。 由 ChatGPT 4.1 翻译