Ehab's Last Corollary

### 题目描述 给出一张 $n$ 个点的无向连通图和一个常数 $k$。 你需要解决以下两个问题的任何一个： 1. 找出一个大小为 $\lceil\frac k2\rceil$ 的独立集。 2. 找出一个大小不超过 $k$ 的环。 独立集是一个点的集合，满足其中任意两点之间在原图上没有边直接相连。 可以证明这两个问题必然有一个可以被解决。 ### 输入格式 第一行三个整数 $n, m, k$。 之后 $m$ 行，每行两个整数 $u, v$，表示在图上有一条 $u, v$ 之间的双向边。 保证 $3\le k\le n\le10^5$，$n-1\le m\le2\times10^5$，$1\le u,v\le n$。 ### 输出格式 第一行输出你解决的问题编号，即 `1` 或 `2`。 若你解决的是问题 1，则第二行需要输出 $\lceil\frac k2\rceil$ 个整数，表示你找到的独立集中点的编号。 否则你需要在第二行输出一个整数 $c$，表示你找到的环的大小，之后第三行输出 $c$ 个整数表示环上的点，你需要保证这 $c$ 个点中相邻的点之间有边。

Given a connected undirected graph with $ n $ vertices and an integer $ k $ , you have to either: - either find an independent set that has exactly $ \lceil\frac{k}{2}\rceil $ vertices. - or find a simple cycle of length at most $ k $ . An independent set is a set of vertices such that no two of them are connected by an edge. A simple cycle is a cycle that doesn't contain any vertex twice. I have a proof that for any input you can always solve at least one of these problems, but it's left as an exercise for the reader.

The first line contains three integers $ n $ , $ m $ , and $ k $ ( $ 3 \le k \le n \le 10^5 $ , $ n-1 \le m \le 2 \cdot 10^5 $ ) — the number of vertices and edges in the graph, and the parameter $ k $ from the statement. Each of the next $ m $ lines contains two integers $ u $ and $ v $ ( $ 1 \le u,v \le n $ ) that mean there's an edge between vertices $ u $ and $ v $ . It's guaranteed that the graph is connected and doesn't contain any self-loops or multiple edges.

If you choose to solve the first problem, then on the first line print $ 1 $ , followed by a line containing $ \lceil\frac{k}{2}\rceil $ distinct integers not exceeding $ n $ , the vertices in the desired independent set. If you, however, choose to solve the second problem, then on the first line print $ 2 $ , followed by a line containing one integer, $ c $ , representing the length of the found cycle, followed by a line containing $ c $ distinct integers not exceeding $ n $ , the vertices in the desired cycle, in the order they appear in the cycle.

4 4 3
1 2
2 3
3 4
4 1

1
1 3

4 5 3
1 2
2 3
3 4
4 1
2 4

2
3
2 3 4

4 6 3
1 2
2 3
3 4
4 1
1 3
2 4

2
3
1 2 3

5 4 5
1 2
1 3
2 4
2 5

1
1 4 5

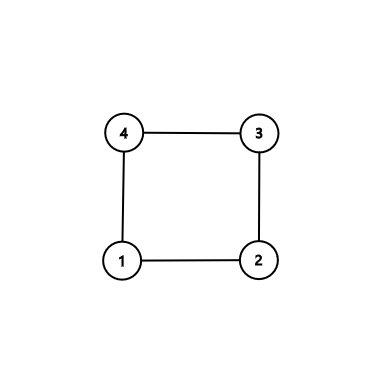
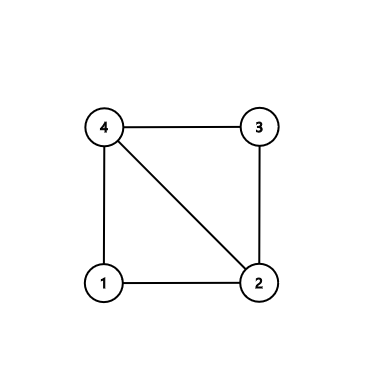
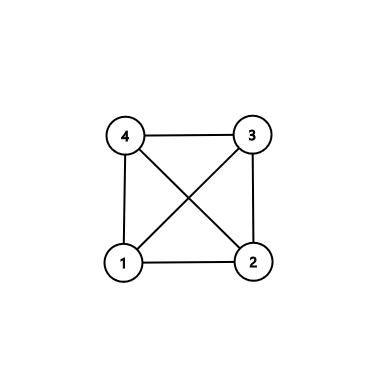
In the first sample:  Notice that printing the independent set $ \{2,4\} $ is also OK, but printing the cycle $ 1-2-3-4 $ isn't, because its length must be at most $ 3 $ . In the second sample:  Notice that printing the independent set $ \{1,3\} $ or printing the cycle $ 2-1-4 $ is also OK. In the third sample:  In the fourth sample: