CF1366F Jog Around The Graph

给定一个简单的带权无向连通图，包含 $n$ 个顶点和 $m$ 条边。 图中长度为 $k$ 的路径定义为一组 $k+1$ 个顶点 $v_1, v_2, \dots, v_{k+1}$，满足对于每个 $i$（$1 \le i \le k$），边 $(v_i, v_{i+1})$ 在图中存在。路径的起点为某个顶点 $v$，即 $v_1 = v$。注意，路径中允许重复经过顶点和边。 路径的权值为路径上所有边的权值之和。 对于每个 $i$ 从 $1$ 到 $q$，考虑从顶点 $1$ 出发、长度为 $i$ 的最大权值路径。请计算这些 $q$ 条路径的权值之和。 由于答案可能很大，请输出对 $10^9+7$ 取模后的结果。

第一行包含三个整数 $n$、$m$、$q$（$2 \le n \le 2000$；$n-1 \le m \le 2000$；$m \le q \le 10^9$），分别表示图的顶点数、边数和需要统计的路径长度数量。 接下来的 $m$ 行，每行包含三个整数 $v$、$u$、$w$（$1 \le v, u \le n$；$1 \le w \le 10^6$），表示顶点 $v$ 和 $u$ 之间有一条权值为 $w$ 的无向边。图中没有自环和重边，且保证图是连通的。

输出一个整数，表示从顶点 $1$ 出发、长度为 $1$ 到 $q$ 的最大权值路径的权值之和，对 $10^9+7$ 取模。

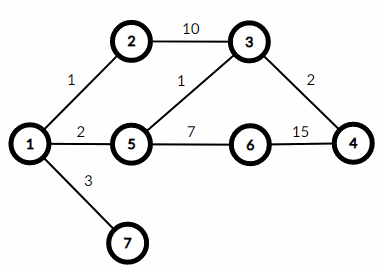
以下是第一个样例的图示：  一些最大权值路径示例： - 长度 $1$：边 $(1, 7)$，权值为 $3$； - 长度 $2$：边 $(1, 2)$、$(2, 3)$，权值为 $1+10=11$； - 长度 $3$：边 $(1, 5)$、$(5, 6)$、$(6, 4)$，权值为 $2+7+15=24$； - 长度 $4$：边 $(1, 5)$、$(5, 6)$、$(6, 4)$、$(6, 4)$，权值为 $2+7+15+15=39$； - $\dots$ 因此答案为前 $25$ 项之和：$3+11+24+39+\dots$ 在第二个样例中，最大权值路径的权值分别为 $4$、$8$、$12$、$16$ 和 $20$。 由 ChatGPT 4.1 翻译