CF1366F Jog Around The Graph

You are given a simple weighted connected undirected graph, consisting of $ n $ vertices and $ m $ edges. A path in the graph of length $ k $ is a sequence of $ k+1 $ vertices $ v_1, v_2, \dots, v_{k+1} $ such that for each $ i $ $ (1 \le i \le k) $ the edge $ (v_i, v_{i+1}) $ is present in the graph. A path from some vertex $ v $ also has vertex $ v_1=v $ . Note that edges and vertices are allowed to be included in the path multiple times. The weight of the path is the total weight of edges in it. For each $ i $ from $ 1 $ to $ q $ consider a path from vertex $ 1 $ of length $ i $ of the maximum weight. What is the sum of weights of these $ q $ paths? Answer can be quite large, so print it modulo $ 10^9+7 $ .

The first line contains a three integers $ n $ , $ m $ , $ q $ ( $ 2 \le n \le 2000 $ ; $ n - 1 \le m \le 2000 $ ; $ m \le q \le 10^9 $ ) — the number of vertices in the graph, the number of edges in the graph and the number of lengths that should be included in the answer. Each of the next $ m $ lines contains a description of an edge: three integers $ v $ , $ u $ , $ w $ ( $ 1 \le v, u \le n $ ; $ 1 \le w \le 10^6 $ ) — two vertices $ v $ and $ u $ are connected by an undirected edge with weight $ w $ . The graph contains no loops and no multiple edges. It is guaranteed that the given edges form a connected graph.

Print a single integer — the sum of the weights of the paths from vertex $ 1 $ of maximum weights of lengths $ 1, 2, \dots, q $ modulo $ 10^9+7 $ .

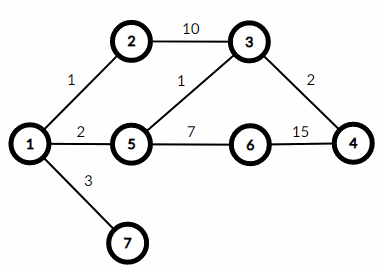Here is the graph for the first example: Some maximum weight paths are: - length $ 1 $ : edges $ (1, 7) $ — weight $ 3 $ ; - length $ 2 $ : edges $ (1, 2), (2, 3) $ — weight $ 1+10=11 $ ; - length $ 3 $ : edges $ (1, 5), (5, 6), (6, 4) $ — weight $ 2+7+15=24 $ ; - length $ 4 $ : edges $ (1, 5), (5, 6), (6, 4), (6, 4) $ — weight $ 2+7+15+15=39 $ ; - $ \dots $ So the answer is the sum of $ 25 $ terms: $ 3+11+24+39+\dots $ In the second example the maximum weight paths have weights $ 4 $ , $ 8 $ , $ 12 $ , $ 16 $ and $ 20 $ .