CF1370F1 The Hidden Pair (Easy Version)

请注意，简单版与困难版的唯一区别在于查询次数的限制。只有在所有版本都被解决后，你才能进行 Hack。 这是一个交互题。 给定一棵包含 $n$ 个节点的树，节点编号为 $1$ 到 $n$。Ayush 和 Ashish 在树中各自选择了两个不同的秘密节点。你需要找出这两个节点。你可以进行如下查询： - 给出一个节点列表，你将收到该列表中某个节点，该节点到两个隐藏节点的距离之和最小（如果有多个这样的节点，则返回其中任意一个）。你还会得到该节点到两个隐藏节点的距离之和。 回忆一下，树是一个无环连通图。两个节点之间的距离定义为它们之间简单路径上的边数。 更正式地，设两个隐藏节点为 $s$ 和 $f$。每次查询你可以提供树上的一个节点集合 $\{a_1, a_2, \ldots, a_c\}$。作为结果，你会得到两个数 $a_i$ 和 $dist(a_i, s) + dist(a_i, f)$。节点 $a_i$ 是你提供的集合中距离之和最小的节点。 你最多可以进行 $14$ 次查询。

第一行包含一个整数 $t$（$1 \leq t \leq 10$），表示测试用例的数量。请注意交互过程的组织方式。 每个测试用例的第一行包含一个整数 $n$（$2 \le n \le 1000$），表示树的节点数。 接下来的 $n-1$ 行，每行包含两个整数 $u$、$v$（$1 \le u, v \le n, u \ne v$），表示树中的一条边。

每次查询请输出一行： - 首先输出 "? c "（不含引号），其中 $c$（$1 \leq c \leq n$）表示查询的节点数，接着输出 $c$ 个 $[1, n]$ 范围内的不同整数，表示要查询的节点编号。 对于每次查询，你将收到两个整数 $x$、$d$，其中 $x$ 是你查询集合中距离之和最小的节点，$d$ 是该节点到两个隐藏节点的距离之和。如果查询的节点集合非法或查询次数超过限制，你将收到 $x = d = -1$，此时应立即终止程序。 当你猜出隐藏节点后，输出一行 "! "（不含引号），后接两个 $[1, n]$ 范围内的整数，表示隐藏节点。两个节点顺序不限。 之后，你需要读取一个字符串。如果猜测正确，你会收到字符串 "Correct"。此时继续解决剩余测试用例或全部结束。如果猜测错误，你会收到字符串 "Incorrect"，此时应立即终止程序。 猜测隐藏节点不计入查询次数。 交互器是非自适应的。隐藏节点不会因查询而改变。 每个测试用例需在输入下一个测试用例前解决。 每个测试用例最多允许 $14$ 次查询，而不是所有测试用例总共 $14$ 次。 每次输出查询后不要忘记换行并刷新输出，否则会因超时被判为 Idleness limit exceeded。可使用： - C++：fflush(stdout) 或 cout.flush() - Java：System.out.flush() - Pascal：flush(output) - Python：stdout.flush() - 其它语言请查阅相关文档。 Hack 格式 如需 Hack，请使用如下输入格式： 第一行包含一个整数 $t$（$1 \leq t \leq 10$），表示测试用例数量。接下来是每个测试用例的描述。 每个测试用例第一行包含一个整数 $n$（$2 \le n \le 1000$），表示树的节点数。第二行包含两个不同的 $[1, n]$ 范围内的整数，表示隐藏节点。接下来的 $n-1$ 行，每行包含两个整数 $u$、$v$（$1 \le u, v \le n, u \ne v$），表示树中的一条边。

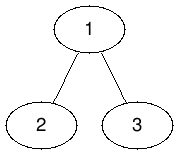
下图为第一个测试用例的树结构，隐藏节点为 $1$ 和 $3$。  由 ChatGPT 4.1 翻译