CF1372E Omkar and Last Floor
题目描述
Omkar 正在建造一座房子。他想要决定如何为最后一层设计地板平面图。
Omkar 的地板最初是 $n$ 行 $m$ 列的全零矩阵($1 \leq n, m \leq 100$)。每一行被划分为若干区间,使得该行的每个 $0$ 恰好属于一个区间。对于每一行的每一个区间,Omkar 可以将该区间内的恰好一个 $0$ 改为 $1$。Omkar 定义地板的“质量”为每一列元素和的平方的总和。即如果第 $i$ 列的元素和为 $q_i$,那么地板的质量为 $\sum_{i=1}^m q_i^2$。
请你帮助 Omkar 求出地板可能达到的最大质量。
输入格式
第一行包含两个整数 $n$ 和 $m$($1 \leq n, m \leq 100$),分别表示行数和列数。
接下来依次描述每一行的区间划分。对于每一行 $i$($1 \leq i \leq n$):
- 首先一行包含一个整数 $k_i$($1 \leq k_i \leq m$),表示第 $i$ 行的区间数。
- 接下来的 $k_i$ 行,每行包含两个整数 $l_{i,j}$ 和 $r_{i,j}$,表示第 $i$ 行第 $j$ 个区间的左右端点(均包含在内)。保证所有区间首尾相接,具体为:$l_{i,1} = 1$,对所有 $1 \leq j \leq k_i$ 有 $l_{i,j} \leq r_{i,j}$,对所有 $2 \leq j \leq k_i$ 有 $r_{i,j-1} + 1 = l_{i,j}$,且 $r_{i,k_i} = m$。
输出格式
输出一个整数,表示可行地板方案的最大可能质量。
说明/提示
给定的测试用例对应如下图示。相同行中相同数字的格子属于同一个区间。
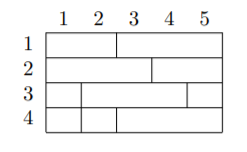
最优的赋值方案如下:
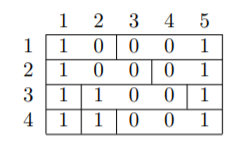
第 $1$ 列的和为 $4$,第 $2$ 列的和为 $2$,第 $3$、$4$ 列的和为 $0$,第 $5$ 列的和为 $4$。
该地板方案的质量为 $4^2 + 2^2 + 0^2 + 0^2 + 4^2 = 36$。你可以证明不存在更高质量的方案。
由 ChatGPT 4.1 翻译