CF1375G Tree Modification

You are given a tree with $ n $ vertices. You are allowed to modify the structure of the tree through the following multi-step operation: 1. Choose three vertices $ a $ , $ b $ , and $ c $ such that $ b $ is adjacent to both $ a $ and $ c $ . 2. For every vertex $ d $ other than $ b $ that is adjacent to $ a $ , remove the edge connecting $ d $ and $ a $ and add the edge connecting $ d $ and $ c $ . 3. Delete the edge connecting $ a $ and $ b $ and add the edge connecting $ a $ and $ c $ . 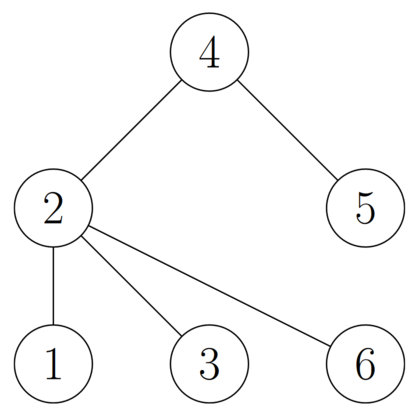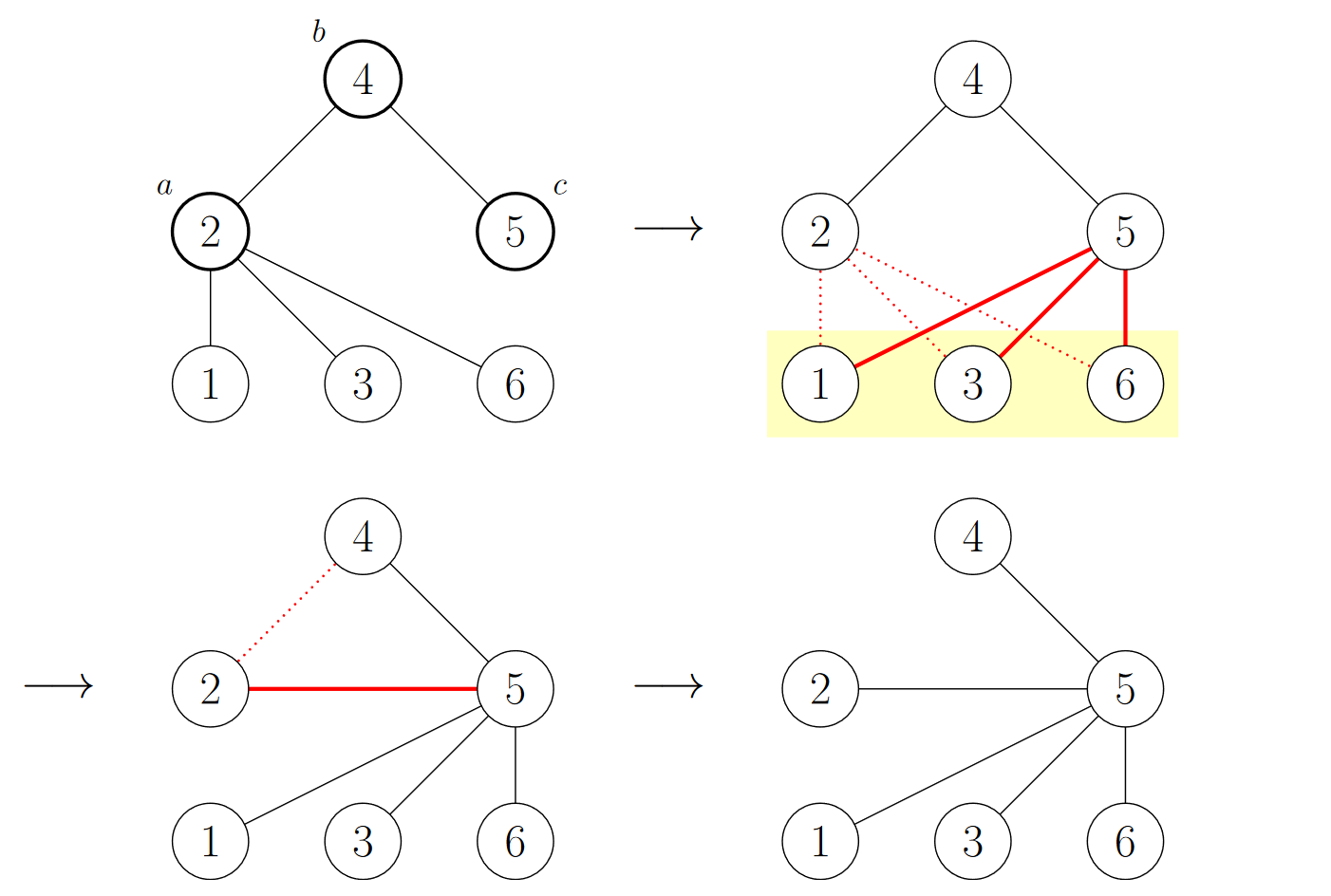As an example, consider the following tree: The following diagram illustrates the sequence of steps that happen when we apply an operation to vertices $ 2 $ , $ 4 $ , and $ 5 $ : It can be proven that after each operation, the resulting graph is still a tree. Find the minimum number of operations that must be performed to transform the tree into a star. A star is a tree with one vertex of degree $ n - 1 $ , called its center, and $ n - 1 $ vertices of degree $ 1 $ .

The first line contains an integer $ n $ ( $ 3 \le n \le 2 \cdot 10^5 $ ) — the number of vertices in the tree. The $ i $ -th of the following $ n - 1 $ lines contains two integers $ u_i $ and $ v_i $ ( $ 1 \le u_i, v_i \le n $ , $ u_i \neq v_i $ ) denoting that there exists an edge connecting vertices $ u_i $ and $ v_i $ . It is guaranteed that the given edges form a tree.

Print a single integer — the minimum number of operations needed to transform the tree into a star. It can be proven that under the given constraints, it is always possible to transform the tree into a star using at most $ 10^{18} $ operations.

The first test case corresponds to the tree shown in the statement. As we have seen before, we can transform the tree into a star with center at vertex $ 5 $ by applying a single operation to vertices $ 2 $ , $ 4 $ , and $ 5 $ . In the second test case, the given tree is already a star with the center at vertex $ 4 $ , so no operations have to be performed.