CF1380F Strange Addition
题目描述
对于非负整数 $a,b$,定义它们的 "奇异加法 $\oplus$" 如下:
1. 将 $a,b$ 一上一下写在两行,并按照低位对齐。
2. 将它们的每一位加起来,并将**每一位的结果从高位到低位连接在一起**,得到的就是 $a\oplus b$。
(你可以认为,两个数都有无穷多的前导 0)
例如,$3248\oplus 908=311416$,因为:
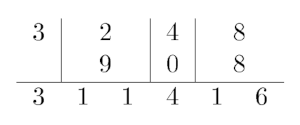
你现在有一个**仅包含 $n$ 个 $0\sim 9$ 的数码**的字符串 $c$,并且还有 $m$ 次操作。一次操作为:
- ```x d``` - 将 $c$ 的第 $x$ 个数码替换成数码 $d$ 。
(注意,$c$ 在任何时刻都可能存在前导 0)
每次操作过后,你需要输出,有多少个**有序对** $(a,b)$,满足 $a,b$ 都是非负整数,且 $a\oplus b=c$。
答案对 $998244353$ 取模。
输入格式
第一行输入两个整数 $n,m$ ( $1\le n,m\le 5\cdot 10^5 $) ,表示 $c$ 的长度和操作次数。
第二行输入 $c$,$c$ 包含 $n$ 个 $0\sim 9$ 的数码。
接下来的 $m$ 行,每行输入两个整数 $x,d$ ( $1\le x\le n,0\le d\le 9$ ) ,表示一次操作。
输出格式
输出共 $m$ 个整数。第 $i$ 个整数表示在前 $i$ 次操作后,有多少个有序对 $(a,b)$ ,满足 $a,b$ 为非负整数且 $a\oplus b=c$ (对 $998244353$ 取模)。
## 样例解释
第一次操作后 $c$ 为 $14$,此时满足条件的 $(a,b)$ 有:$(0,14),(1, 13),(2, 12),(3, 11),(4, 10),(5, 9),(6, 8),(7, 7),(8, 6),(9, 5)(10, 4),(11, 3),(12, 2),(13, 1),(14, 0)$
第二次操作后 $c$ 为 $11$。第三次后 $c$ 为 $01$ 。
说明/提示
After the first update $ c $ is equal to $ 14 $ . The pairs that sum up to $ 14 $ are: $ (0, 14) $ , $ (1, 13) $ , $ (2, 12) $ , $ (3, 11) $ , $ (4, 10) $ , $ (5, 9) $ , $ (6, 8) $ , $ (7, 7) $ , $ (8, 6) $ , $ (9, 5) $ , $ (10, 4) $ , $ (11, 3) $ , $ (12, 2) $ , $ (13, 1) $ , $ (14, 0) $ .
After the second update $ c $ is equal to $ 11 $ .
After the third update $ c $ is equal to $ 01 $ .