CF1380F Strange Addition

Let $ a $ and $ b $ be some non-negative integers. Let's define strange addition of $ a $ and $ b $ as following: 1. write down the numbers one under another and align them by their least significant digit; 2. add them up digit by digit and concatenate the respective sums together. Assume that both numbers have an infinite number of leading zeros. 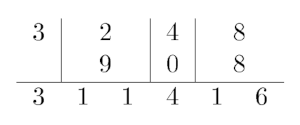For example, let's take a look at a strange addition of numbers $ 3248 $ and $ 908 $ : You are given a string $ c $ , consisting of $ n $ digits from $ 0 $ to $ 9 $ . You are also given $ m $ updates of form: - $ x~d $ — replace the digit at the $ x $ -th position of $ c $ with a digit $ d $ . Note that string $ c $ might have leading zeros at any point of time. After each update print the number of pairs $ (a, b) $ such that both $ a $ and $ b $ are non-negative integers and the result of a strange addition of $ a $ and $ b $ is equal to $ c $ . Note that the numbers of pairs can be quite large, so print them modulo $ 998244353 $ .

The first line contains two integers $ n $ and $ m $ ( $ 1 \le n, m \le 5 \cdot 10^5 $ ) — the length of the number $ c $ and the number of updates. The second line contains a string $ c $ , consisting of exactly $ n $ digits from $ 0 $ to $ 9 $ . Each of the next $ m $ lines contains two integers $ x $ and $ d $ ( $ 1 \le x \le n $ , $ 0 \le d \le 9 $ ) — the descriptions of updates.

Print $ m $ integers — the $ i $ -th value should be equal to the number of pairs $ (a, b) $ such that both $ a $ and $ b $ are non-negative integers and the result of a strange addition of $ a $ and $ b $ is equal to $ c $ after $ i $ updates are applied. Note that the numbers of pairs can be quite large, so print them modulo $ 998244353 $ .

After the first update $ c $ is equal to $ 14 $ . The pairs that sum up to $ 14 $ are: $ (0, 14) $ , $ (1, 13) $ , $ (2, 12) $ , $ (3, 11) $ , $ (4, 10) $ , $ (5, 9) $ , $ (6, 8) $ , $ (7, 7) $ , $ (8, 6) $ , $ (9, 5) $ , $ (10, 4) $ , $ (11, 3) $ , $ (12, 2) $ , $ (13, 1) $ , $ (14, 0) $ . After the second update $ c $ is equal to $ 11 $ . After the third update $ c $ is equal to $ 01 $ .