CF1381D The Majestic Brown Tree Snake

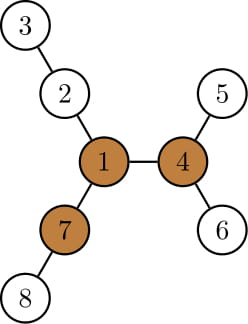
有一棵包含 $n$ 个顶点的无向树，由 $n-1$ 条双向边连接。现在有一条蛇卡在这棵树中。蛇的头在顶点 $a$，尾在顶点 $b$。蛇的身体占据了从 $a$ 到 $b$ 的唯一一条简单路径上的所有顶点。 蛇想知道它是否可以将自己反转——也就是说，能否让它的头移动到原来尾所在的位置，尾移动到原来头所在的位置。遗憾的是，蛇的移动受到树结构的限制。 在一次操作中，蛇可以将头移动到一个未被蛇占据的相邻顶点。此时，尾会向头靠近一个顶点，以保持蛇的长度不变。同理，蛇也可以将尾移动到一个未被蛇占据的相邻顶点，此时头会向尾靠近一个顶点。  我们用 $(h, t)$ 表示蛇的位置，其中 $h$ 表示蛇头所在顶点的编号，$t$ 表示蛇尾所在顶点的编号。对于上图中的蛇，可以通过如下操作实现反转： $(4,7)\to (5,1)\to (4,2)\to (1,3)\to (7,2)\to (8,1)\to (7,4)$。 请判断是否存在一系列操作，使得蛇能够完成反转。

第一行包含一个整数 $t$（$1\le t\le 100$），表示测试用例的数量。接下来是每个测试用例的描述。 每个测试用例的第一行包含三个整数 $n,a,b$（$2\le n\le 10^5,1\le a,b\le n,a\ne b$）。 接下来的 $n-1$ 行，每行包含两个整数 $u_i,v_i$（$1\le u_i,v_i\le n,u_i\ne v_i$），表示顶点 $u_i$ 和 $v_i$ 之间有一条边。保证给定的边构成一棵树。 保证所有测试用例中 $n$ 的总和不超过 $10^5$。

对于每个测试用例，如果蛇能够完成反转，输出 "YES"；否则输出 "NO"。

第一个测试用例如上图所示。 在第二个测试用例中，树是一条链。可以证明蛇无法完成反转。 在第三个测试用例中，也可以证明蛇无法完成反转。 在第四个测试用例中，以下是一种可行的操作序列： $(15,12)\to (16,11)\to (15,13)\to (10,14)\to (8,13)\to (4,11)\to (1,10)$ $\to (2,8)\to (3,4)\to (2,5)\to (1,6)\to (4,7)\to (8,6)\to (10,5)$ $\to (11,4)\to (13,8)\to (14,10)\to (13,15)\to (11,16)\to (12,15)$。 由 ChatGPT 4.1 翻译