CF1381E Origami
题目描述
在被一个丑陋的几何题连续 13 次超时打击后,你决定休息一下,做点手工艺放松心情。
现在有一张纸,它的形状是一个简单多边形,共有 $n$ 个顶点。这个多边形可能不是凸多边形,但我们都知道,合格的折纸纸张有一个性质:任意一条水平直线与多边形的边界最多相交两次。
如果你沿着竖直直线 $x=f$ 折叠纸张,折叠后形成的图形面积是多少?折叠时,直线左侧的部分会关于该直线对称地反射到右侧。
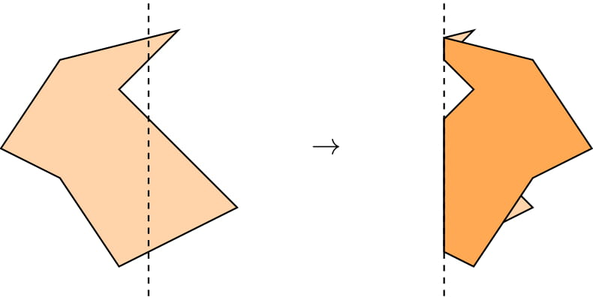
你的任务是回答 $q$ 个独立的询问,每个询问给出一个折叠位置 $f_1,\ldots,f_q$。
输入格式
第一行包含两个整数 $n$、$q$($3\le n\le 10^5, 1\le q\le 10^5$),分别表示多边形的顶点数和询问数。
接下来的 $n$ 行,每行包含两个整数 $x_i$、$y_i$($|x_i|, |y_i|\le 10^5$),表示多边形第 $i$ 个顶点的坐标。多边形的每一对相邻点之间有一条边,且 $(x_1, y_1)$ 与 $(x_n, y_n)$ 之间也有一条边。保证多边形非退化,且任意一条水平直线与多边形边界最多相交两次。特别地,没有边是严格水平的。相邻的两条边可以共线。
接下来的 $q$ 行,每行包含一个整数 $f_i$($\min\limits_{j=1}^n(x_j)< f_i< \max\limits_{j=1}^n(x_j)$),表示第 $i$ 次折叠的 $x$ 坐标。保证所有 $f_i$ 互不相同。
输出格式
对于每个询问,输出折叠后纸张的面积 $A_i$。
你的答案被认为是正确的,当且仅当其绝对误差或相对误差不超过 $10^{-4}$。
形式化地,设你的答案为 $a$,标准答案为 $b$,当且仅当 $\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-4}$ 时,答案被接受。
说明/提示
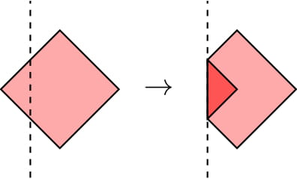
第一个测试,折叠线 $f=-5$:
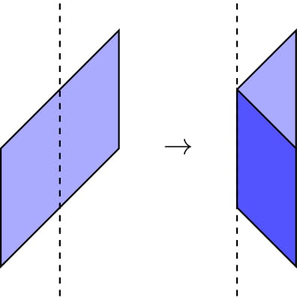
第二个测试,折叠线 $f=1$:
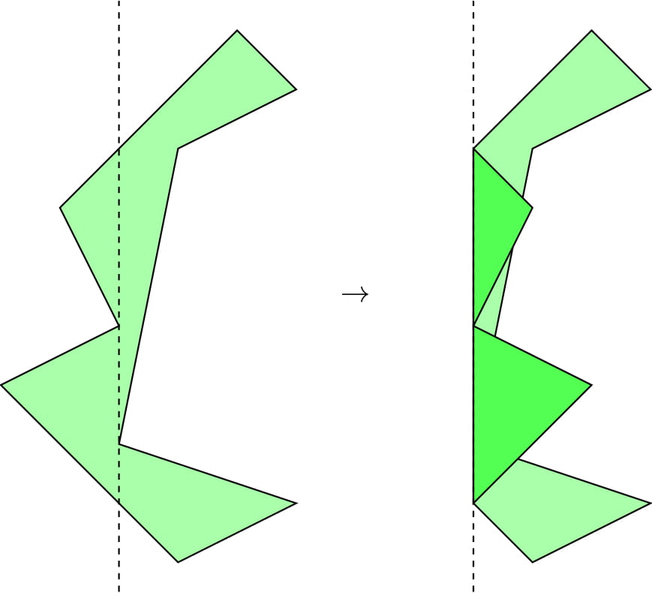
第三个测试,折叠线 $f=-1$:
由 ChatGPT 4.1 翻译