CF1383F Special Edges

考拉 Koa 有一个有向图 $G$，包含 $n$ 个点和 $m$ 条边。每条边都有一个容量。图中恰好有 $k$ 条特殊边（编号为 $1$ 到 $k$），这些特殊边的初始容量均为 $0$。 Koa 会向你提出 $q$ 个询问。每次询问，她会给出 $k$ 个整数 $w_1, w_2, \ldots, w_k$，表示将第 $i$ 条特殊边的容量设置为 $w_i$（其他边的容量保持不变）。 Koa 想知道：在每次询问后，从节点 $1$ 到节点 $n$ 的最大流是多少？ 请你帮助她解决这个问题。

输入的第一行包含四个整数 $n$、$m$、$k$、$q$（$2 \le n \le 10^4$，$1 \le m \le 10^4$，$1 \le k \le \min(10, m)$，$1 \le q \le 2 \times 10^5$），分别表示节点数、边数、特殊边数和询问数。 接下来的 $m$ 行，每行包含三个整数 $u$、$v$、$w$（$1 \le u, v \le n$，$0 \le w \le 25$），表示一条从 $u$ 到 $v$ 的有向边，容量为 $w$。 边的编号按照输入顺序从 $1$ 开始。前 $k$ 条边为特殊边。保证对于所有 $1 \le i \le k$，都有 $w_i = 0$。 接下来的 $q$ 行，每行包含 $k$ 个整数 $w_1, w_2, \ldots, w_k$（$0 \le w_i \le 25$），表示本次询问中每条特殊边的容量。

对于第 $i$ 个询问，输出一个整数 $res_i$，表示在本次询问下，从节点 $1$ 到节点 $n$ 的最大流。

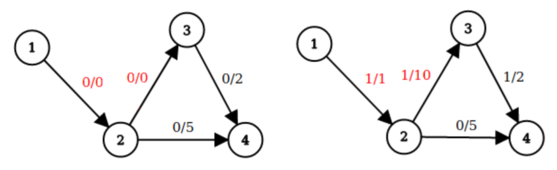
对于第二个样例，以下图片分别对应前两个询问（从左到右）。每条边上标注了“流量/容量”，特殊边用红色表示。  如图所示，第一个询问时，从节点 $1$ 到节点 $4$ 的最大流为 $0$，第二个询问时最大流为 $1$。 由 ChatGPT 4.1 翻译