CF1386C Joker

Joker 回到哥谭市，准备实施又一个邪恶计划。在哥谭市中，有 $N$ 个街道交叉口（编号从 $1$ 到 $N$），以及 $M$ 条街道（编号从 $1$ 到 $M$）。每条街道连接两个不同的交叉口，且任意两个交叉口之间最多只会有一条街道相连。 为了他的邪恶计划，Joker 需要使用奇数条街道组成一个环。也就是说，存在某个交叉口 $S$ 和一个正偶数 $k$，使得存在一条交叉口序列 $S, s_1, \ldots, s_k, S$，满足以下条件：存在街道连接 (a) $S$ 和 $s_1$，(b) $s_k$ 和 $S$，以及 (c) 对于每个 $i = 2, \ldots, k$，$s_{i-1}$ 和 $s_i$ 之间有街道相连。 然而，警方正在管控哥谭市的街道。在第 $i$ 天，警方会监控一组编号连续的街道 $j$，即 $l_i \leq j \leq r_i$。这些被监控的街道当然不能被 Joker 用来实施计划。不幸的是，Joker 在哥谭市警察局内部有间谍，他们会告诉他每天哪些街道被监控。现在 Joker 想知道，在给定的若干天中，他是否能够实施他的邪恶计划。也就是说，在某一天，是否存在一条由奇数条未被监控街道组成的环。

输入的第一行包含三个整数 $N$、$M$ 和 $Q$（$1 \leq N, M, Q \leq 200\,000$），分别表示交叉口数量、街道数量和需要查询的天数。接下来的 $M$ 行描述街道，第 $j$ 行（$1 \leq j \leq M$）包含两个交叉口编号 $u$ 和 $v$（$u \neq v$），表示第 $j$ 条街道连接这两个交叉口。保证任意两个交叉口之间最多只有一条街道相连。接下来的 $Q$ 行，每行包含两个整数 $l_i$ 和 $r_i$，表示在第 $i$ 天，所有编号为 $l_i \leq j \leq r_i$ 的街道都被警方监控（$1 \leq i \leq Q$）。

输出共 $Q$ 行。第 $i$ 行（$1 \leq i \leq Q$）输出 "YES" 如果 Joker 能在第 $i$ 天实施计划，否则输出 "NO"。

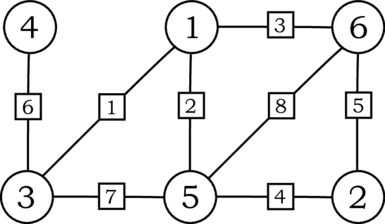
示例测试中的图如下：  由 ChatGPT 4.1 翻译