CF1388E Uncle Bogdan and Projections

回到岸上后，Bogdan 叔叔通常会去计算机俱乐部“The Rock”，在愉快的氛围中解题。一天，Bogdan 叔叔遇到了他多年的老朋友，朋友给他讲了一个不同寻常的问题…… 在平面直角坐标系中，有 $n$ 条两两不相交的水平线段，且端点均为整数点。所有线段都严格位于 $OX$ 轴的上方，即全部在第一象限和第四象限。你可以任选一个向量 $(a, b)$，其中 $b < 0$，且 $a, b$ 为实数，然后沿该向量将所有线段投影到 $OX$ 轴上，形式化地说，$\forall (x,y)$ 在一条线段上，其在 $OX$ 轴上的投影为 $(x-a\frac{y}{b},0)$。投影后的线段不能相交，但可以相切。 请你求出右侧最右端投影的 $x$ 坐标与左侧最左端投影的 $x$ 坐标的最小可能差值。

第一行包含一个整数 $n$（$1 \le n \le 2000$），表示线段的数量。 接下来的 $n$ 行中，第 $i$ 行包含三个整数 $xl_i$、$xr_i$ 和 $y_i$（$-10^6 \le xl_i < xr_i \le 10^6$；$1 \le y_i \le 10^6$），表示第 $i$ 条线段的坐标。 保证所有线段互不相交且不相切。

输出你能得到的最小可能差值。 如果你的答案的绝对误差或相对误差不超过 $10^{-6}$，则视为正确。 形式化地说，若你的答案为 $a$，标准答案为 $b$，则当 $\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-6}$ 时，视为正确。

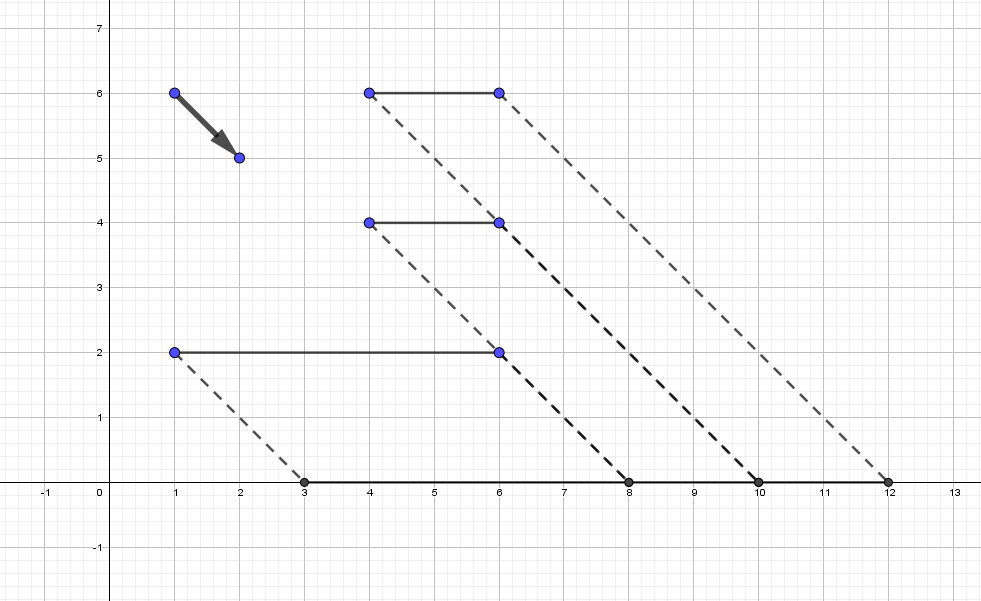
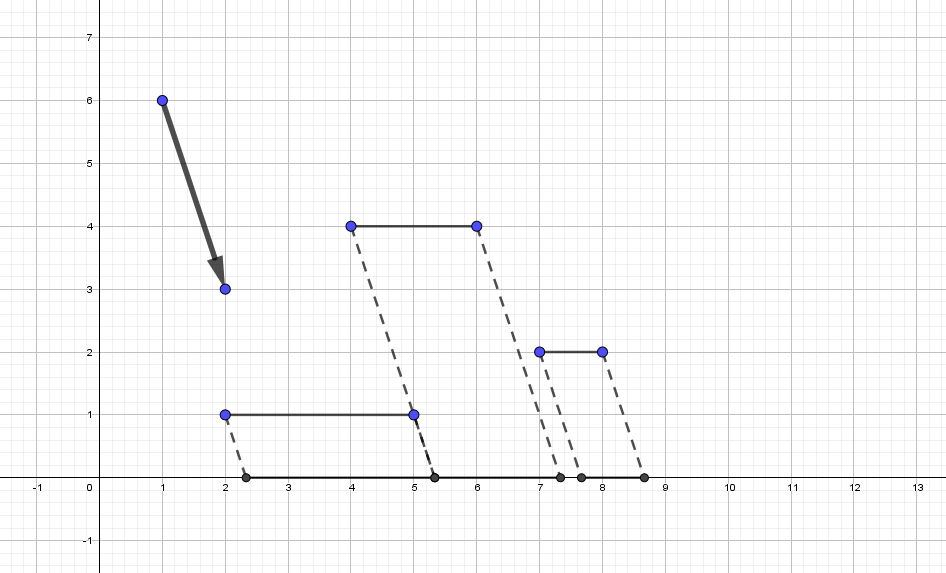
在第一个样例中，如果沿向量 $(1, -1)$ 投影，则答案为 $12-3=9$，且可以证明无法得到更小的值。  在第二个样例中，最优投影向量为 $(1, -3)$。答案为 $8\frac{2}{3}-2\frac{1}{3}=6\frac{1}{3}$。  由 ChatGPT 4.1 翻译